Для ускорения работы поступают так. По внешней окружности транспортира отмечают направления на все пикеты. Рядом с каждой точкой ставят номер. Если есть углы более 1800, транспортир перекладывают, поворачивая его на 1800. После этого по нему отмечают значения угла минус 1800. Когда все углы отмечены, транспортир снимают. Из станции, как из центра, на все точки проводят лучи и откладывают расстояния. Конец каждого отложенного расстояния дает положение точки. Точку изображают кружком, рядом выписывают из журнала его отметку.

Вместо транспортира применяют также линейки-тахеографы. Они представляют собой прозрачный круг с разграфкой от 0 до 3590. По отметкам станций и реечных точек на плане проводят горизонтали с принятым сечением рельефа. Следы горизонталей отыскивают графической интерполяцией между точками, которые в абрисе соединены стрелками. Соединение каких-либо двух точек в абрисе говорит о том, что местность между ними имеет один скат, без перегибов.

Все контуры и рельеф, изображаемые на плане, вычерчивают тушью в соответствии с условными знаками. Над северной рамкой делают заглавную надпись, под южной рамкой подписывают числовой масштаб, высоту сечения рельефа, вычерчивают линейный масштаб и график заложений.

Автоматизация тахеометрической съемки

С появлением электронных тахеометров стала возможна частичная или полная автоматизация тахеометрической съемки.

При съемке электронный тахеометр устанавливается на съемочных точках, а на пикетных точках – специальные вешки с отражателями, входящими в комплект тахеометра. При наведении на отражатели вешки в автоматическом режиме определяются горизонтальные и вертикальные углы, а также расстояние у смежных съемочных и пикетных точек. С помощью микроЭВМ тахеометры производят обработку результатов измерений и в итоге получают приращения ∆х и ∆у координаты превышения h и смежные съемочные и пикетные точки. При этом автоматически учитываются все поправки в измеряемые расстояния и за наклон вертикальной оси прибора в измеряемые углы. Результаты измерений могут быть введены в специальное запоминающее устройство (накопитель информации) или переписанные в магнитную кассету. В дальнейшем из накопителя или магнитной кассеты информация поступает в ЭВМ, которая по специальной программе производит окончательную обработку результатов измерений, включающую вычисление координат съемочных и пикетных точек, уравнивание съемочного хода и другие вычисления, необходимое для графического построения топографического плана или цифровой модели местности. Графическое построение топографического плана осуществляется графопостроителем, соединенным с ЭВМ.

2.4 Способы прямой и обратной угловых засечек

Засечкой называется метод определения координат отдельной точки измерением элементов, связывающих ее положение с исходными пунктами.

Для определения планового положения точки необходимо измерить два элемента. Для контроля, кроме необходимых, выполняют избыточные измерения. Засечки различают прямые, обратные и комбинированные. В прямой засечке измерения выполняют на исходных пунктах (рис. 6.6 a, г); в обратной – на определяемом пункте (рис. 6.6 б, д); в комбинированной – на исходных и определяемом пунктах (рис. 6.6 в). В зависимости от вида измерений засечки бывают угловые (рис. 6.6 a, б, в), линейные (рис. 6.6 г), линейно-угловые (рис. 6.6 д). Измеренные углы на рис. 6.6 отмечены дугами, измеренные расстояния – двумя штрихами.

Рассмотрим вычисление координат в некоторых засечках.

Прямая угловая засечка. На исходных пунктах A и B с координатами , , , . (рис. 6.6 а)измеряют углы и . При обработке измерений сначала вычисляют дирекционные углы направлений AP и BP:

; .

Дирекционные углы с координатами связаны формулами обратной геодезической задачи

; .

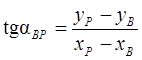Решая эти уравнения относительно xp и yp, получим формулы, по которым вычисляют координаты определяемой точки Р (формулы Гаусса):

;

.

Для контроля ординату yP вычисляют вторично по формуле:

.

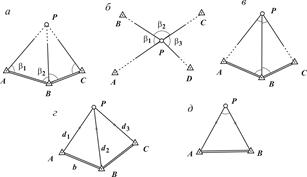
Рис. 7. Схемы засечек: а – прямая угловая; б – обратная угловая; в – комбинированная угловая; г – линейная; д – линейно-угловая

Если один из дирекционных углов или близок к или , то вместо формул выше вычисления выполняют по формулам

;

.

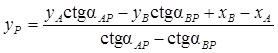Для контроля аналогичные измерения и вычисления выполняют, опираясь на другую исходную сторону BC. За окончательные значения координат определяемой точки принимают средние.

Существуют и иные формулы решения прямой угловой засечки, например, формулы котангенсов углов треугольника (формулы Юнга):

; .

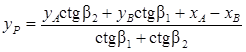Обратная угловая засечка.

На определяемой точке P (рис. 6.6 б) измеряют углы и между направлениями на исходные пункты A, B и C. При этом исходные пункты выбирают такие, чтобы они с точкой P не оказались на одной окружности или вблизи нее. Координаты точки P вычисляют по формулам Гаусса (6.5 - 6.7), предварительно вычислив дирекционные углы:

; .

Для контроля измеряют избыточный угол и вычисляют координаты, используя другую пару измеренных углов.

Линейная засечка. Для определения координат точки Р (рис. 6.6 г) измеряют расстояния d1, d2. По формуле косинусов (6.1) находят углы треугольника АРВ. Вычисляют дирекционный угол aАР = aАВ - ÐA, а затем по формулам прямой геодезической задачи - искомые координаты