- предусматривается возможность привязки ходов к пунктам высшего класса; если к исходному пункту нельзя примкнуть непосредственно, составляют проект передачи координат с него на пункт полигонометрии с учетом указаний;

- полигонометрические ходы должны быть по возможности вытянутыми и равносторонними; короткие стороны не следует располагать рядом с длинными; практически ход считается вытянутым, если пункты его расположены вправо или влево от замыкающей не более чем на 1/10 ее длины, а стороны составляют с замыкающей углы не более 200;

- для ходов с большим числом подсчитывают ожидаемую линейную невязку М'; если относительная невязка окажется больше допустимой, проект следует изменить. Следует отметить, что величина относительной невязки полигонометрического хода не всегда является достаточным критерием точности определения координат пунктов, поэтому в отдельных случаях при проектировании ломанных ходов целесообразно вычислять ожидаемую ошибку определения отдельных пунктов.

Полигонометрические сети 4 класса создают в виде системы или отдельных ходов. Проложение замкнутых ходов, опирающихся на один исходный пункт, и висящих ходов не допускается.

Полигонометрические сети, развиваемые на территориях городов, поселков, горнодобывающей и нефтеперерабатывающих предприятий, для строительства инженерных сооружений должны удовлетворять требованиям, приведенным в таблице 2.

3.5 Оценка точности полигонометрической сети методом последовательных приближений

Оценка проектов полигонометрических сетей заключается в определении ожидаемых ошибок координат узловых пунктов, относительных ошибок ходов и сравнении их с допустимыми. Выполняется строгими и приближенными способами. Для оценки проектов полигонометрических сетей наиболее простым является методом последовательных приближений. Этот метод дает возможность подсчитать ожидаемую среднюю квадратическую ошибку определения положения каждой узловой точки по отношению к группе смежных узловых точек, а не по отношению к исходным пунктам. Для начала оценки необходимо произвести линейные измерения. Для этого измеряются длины линий в ходах, сходящихся в узловых точках I и II. Сеть относится к полигонометрии 4 класса. Измерение линий предполагается произвести светодальномером, поэтому средняя квадратическая ошибка измерения линий принята mS = ±15 мм, а ошибка угла mβ = ±2''. Вычисленные длины линий представлены в таблице 5.

Таблица 5

Ожидаемые ошибки определения конечных точек каждого хода вычисляют по формуле:

(13)

где n – количество линий в ходе; [S] – длина хода; mS - средняя квадратическая ошибка измерения линии; mβ - средняя квадратическая ошибка измерения угла.

Вычисленные средние ожидаемые ошибки определения положения конечных точек хода по формуле (13) представлены в таблице 6.

Таблица 6

Веса определения положения узловых точек I и II по соответствующим ходам r1, r2 и r3; r3, r4 и r5 вычисляются по формулам:

для I узловой точки:

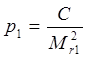
для II узловой точки: (14)

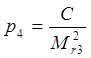
где С – постоянная величина и равна 100000.

Общий вес определения положения узловых точек I и II будет равно:

Р1= Р1 +Р2+ Р3; Р2 =Р3 +Р4+ Р5 (15)

Средние квадратические ошибки определятся формулой:

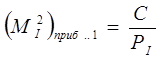
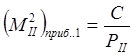
Во 2-м приближении полученные среднеквадратические ошибки узловых точек I и II следует учесть как ошибки исходных данных. Следовательно, для I узловой точки получим:

(17)

Веса по ходам во втором приближении находятся аналогично. Приведенные вычисления сводятся в таблицу 7. Приближения производятся до тех пор, пока результаты оценки в последних двух приближениях не совпадут.

Таблица 7 – Метод последовательных приближений