4.6 Расчёт пустотной плиты по предельным состояниям

Усилия от расчетных и нормативных нагрузок. От расчетной нагрузки:

От нормативной полной нагрузки:

От нормативной постоянной длительной:

4.7 Установление размеров сечения плиты

Высота сечения многопустотной предварительно напряженной плиты h =22 см; рабочая высота сечения h0=h-a=22-3=19 см; толщина верхней полки 3,1см; нижней -3см. Ширина рёбер: средних 3,2см, крайних- 4.1см. В расчетах по предельным состояниям первой группы расчетная толщина сжатой полки таврового сечения h’f=3,0 cм; отношение h’f/h=3,0/22= =0.14 >0.1, при этом в расчет вводится вся ширина полки b’f=196 cм; расчетная ширина ребра: b=196-10×15,9=37 см.

4.8 Расчет прочности плиты по сечению, нормальному к продольной оси,М=60.5295 кН×м

Сечение тавровое с полкой в сжатой зоне.

Вычисляем:

здесь SR=Rs=680+400-588.75=491.25 МПа; в знаменателе формулы принято 500 МПа, поскольку b2<1.

Коэффициент условий работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести, согласно формуле:

см2.

Принимаем 10 стержней  8 мм с Аs=5.03 см2.

4.9 Расчет прочности плиты по сечению, наклонному к продольной оси, Q=43.7827 кН

Влияние усилия обжатия P= 245.84 кH:

Проверяем, требуется ли поперечная арматура по расчёту.

Условие:

Qmax=43.7827×103 Н<2,5×Rbt×b×h0=2,5×0,9×1,05×(100)×37×19=166×103 Н – удовлетворяется.

При

и поскольку

0,16×jb4×(1+jn)×Rbt×b=0,16×1,5×(1+0,333)×0,9×1,05×37×100=1118.6Н/см >118.446 Н/см,

принимают с=2,5×h0=2,5×19= 47,5 см.

Другое условие: при

Q = Qmax – q1×c = 43.7827×103 – 118.446×47,5 = 38.1565×103 H,

- удовлетворяется.

Следовательно, поперечной арматуры по расчёту не требуется.

На приопорных участках длиной l/4 арматуру устанавливают конструктивно, в средней части пролёта поперечная арматура не применяется.

4.10 Расчет пустотной плиты по предельным состояниям второй группы

Геометрические характеристики приведенного сечения. Круглое очертание пустот заменяют эквивалентным квадратным со стороной:

h=0.9d=0,9·15,9=14,31см.

Толщина полок эквивалентного сечения: h’f=h=(22-14,31) ·0,5=3,845см.

Ширина ребра 196-9·14,31=52.9 см.

Ширина пустот 196-42.9=143.1 см.

Площадь приведённого сечения Ared=196·22-143.1·14,31=2264.239 см2. Расстояние от нижней грани до центра тяжести приведённого сечения: y0=0,5h=0,5·22=11см. Момент инерции сечения (симметричного):

см4.

Момент сопротивления сечения по нижней зоне:

см3;

то же, по верхней зоне см3.

Расстояние от ядровой точки, наиболее удалённой от растянутой зоны (верхней), до центра тяжести сечения по формуле

cм;

то же, наименее удалённой от растянутой зоны (нижней) rinf =4,74 см. Упругопластический момент сопротивления по растянутой зоне согласно формуле:

см3,

здесь γ=1,5 для двутаврового сечения.

Упругопластический момент по растянутой зоне в стадии изготовления и обжатия W’pl=18950.85 см3.

Потери предварительного напряжения арматуры.

Коэффициент точности натяжения арматуры p=1. Потери от релаксации напряжений в арматуре при электротермическом способе натяжения:

Потери от температурного перепада между натянутой арматурой и упорами, так как при пропаривании форма с упорами нагревается вместе с изделием.

Эксцентриситет этого усилия относительно центра тяжести приведенного сечения:

eop=y0-d=11-3 = 8 см

Напряжение в бетоне при обжатии:

МПа

Устанавливаем величину передаточной прочности бетона из условия:

Rbp=3.09/0,75=4.12<0.5×B25=12,5 МПа

Принимаем Rbp=12,5МПа. Тогда отношение

bp/Rbp=3.09/12,5=0,2472.

Вычисляем сжимающее напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия Р1 (без учета изгибающего момента от веса плиты):

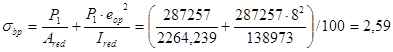МПа

Потери от быстронатекающей ползучести при

bp/Rbp=2.59/12,5=0.2072

С учетом потерь:

Р1=Аs×(sp-los1)=5.03×(588.75-25.9505)×(100)=283088 H

МПа;

Усилие обжатия с учетом полных потерь:

Р2=Аs×(sp-los)=5.03×(588.75-100)×(100)=245,84 кН

Расчет по образованию трещин, нормальных к продольной оси

Производится для выяснения необходимости проверки по раскрытию трещин. Коэффициент надежности по нагрузке f=1; М=52,1481 кН×м.

Вычисляем момент образования трещин по приближенному способу ядровых моментов:

Mcrc=Rbt,ser×Wpl+Mrp=1.6×18950,85×(100)+ 2818801,44 =58,51 кН×м

Здесь ядровый момент усилия обжатия при sp=0.9:

Mrp=sp×P2×(eop+r)=0.9×245840×(8+4.74)=2818801,44 H×см

поскольку М=52,1481<Mcrc=58,51 кН×м, трещины в растянутой зоне не образуются. Следовательно, нет необходимости в расчете по раскрытию трещин.

Проверим, образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении коэффициента точности натяжения sp=1.10 (момент от веса плиты не учитывается).

Расчетное условие:

sp×P1×(eop-rinf)-M<Rbtp×W’pl

1.10×287257×(8-4,74) =1030103,602 H×см

1×18950,85×(100)=1895085 H×см

1030103,602 H×см <1895085 H×см

Условие удовлетворяется, начальные трещины не образуются.

здесь Rbtp=1МПа - сопротивление бетона растяжению, соответствующее передаточной прочности бетона Rbp=12.5 МПа.

Расчет прогиба плиты. Прогиб определяется от нормативного значения постоянной и длительной нагрузок, предельный прогиб