Этот закон гласит: скорость изменения количества движения любой части материальной системы, находящейся в движении, равна сумме всех внешних сил. В математическом виде этот закон запишется так:

(1)

где (2)

Fv – силы обусловленные силовыми полями

Fs – силы действующие на единицу поверхности.

Подставив (2) в (1) получим интегральную форму записи закона сохранения количества движения

. (3)

Это векторное уравнение эквивалентно системе из трех уравнений, отражающих закон сохранения количества движения по каждой из координат х1, х2, х3

(4)

Пользуясь правилами дифференцирования интеграла, взятого по изменяющемуся объему и объединяя два слагаемых, получим

. (5)

Учитывая приведем (5) к виду

. (6)

Поскольку это равенство справедливо при произвольном объеме подынтегральное выражение (6) должно быть равно нулю

. (7)

Выражение (7) есть дифференциальная форма записи закона сохранения количества движения.

Для одномерного случая, когда все составляющие сил и скоростей по всем направлениям, кроме оси х1, равны нулю, уравнения (5) и (7) примет вид

.

Для написания математической модели линейного нефтепровода будем пользоваться этими двумя законами.

Дифференциальная форма записи линейного нефтепровода.

Рассмотрим динамическую модель нефтепровода. Запишем исходные уравнения законов сохранения массы и количества движения в интегральной форме

(1)

(2)

В качестве объема W выберем цилиндр, вырезанный из потока двумя перпендикулярными к оси трубы сечениями, отстоящими друг от друга на расстоянии DХ1. Считая DХ1 малой величиной, уравнения можно записать в виде

(3)

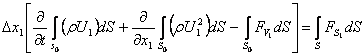(4)

где S0 – площадь основания выделенного цилиндра

; d – диаметр трубы.

Считая величины и постоянными по сечению и переходя к средней скорости потока v по сечению трубы по правилу

. (5)

Из уравнений (3) и (4) получим.

(6)

(7)

Коэффициент введен для учета профиля скорости по сечению трубы. Для ламинарного течения .

Сила определяется полем сил тяжести

. (8)

Силу , действующую на поверхность объема интегрирования, разделим на две составляющие:

- сила, обусловленная разностью давлений на основании цилиндра

- сила, определяемая трением объема стенки

(9)

здесь - боковая поверхность цилиндра

- касательное напряжение трения на стенке трубы

; - коэффициент сопротивления.

Раскладывая в ряд Тейлора и ограничившись первыми двумя членами, получим.

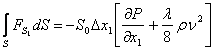(10)

Подставив (8) и (10) в (7), запишем законы сохранения массы и количества движения для движения жидкости по нефтепроводу в следующем виде:

(11)

(12)

Введем дополнительное уравнение. Это соотношение между скоростями изменения плотности и давления:

(13)

где С – скорость звука в жидкости.

Второе уравнение можно упростить объединив слагаемые и . Такое упрощение возможно, если принять суммарное давление в точке х равным , где - высота подъема трубопровода от нулевой точки. В нашем случае . Слагаемое - характеризует изменение давления вдоль трубопровода за счет скорости напора.

Для несжимаемой жидкости, когда и вдоль трубы постоянны, это слагаемое равно нулю. Учитывая уравнение (13), получим обычно используемую математическую модель для описания движения жидкости в линейном трубопроводе:

(14)

Система уравнений (14) нелинейна.

Линеаризуем эту систему, приняв во внимание