Глава 3. Основные уравнения.

Согласно [7], запишем систему уравнений для нахождения Âкр.:

Dv - Ñw + Âtn = 0

Dt = - vz (3.1)

div v = 0,

где t - малое возмущение температуры, w - малое возмущение квадратичной скорости, n – единичный вектор в напралении оси z, - вертикально вверх

Приводим систему (3.1) к одному уравнению. Применив к первому уравнению операцию rotrot = Ñdiv - D, взяв затем его z – компоненту, получим:

D3t = ÂD2t, (3.2)

(где D2 = ¶2/¶х2 + ¶2/¶у2 – двухмерный лапласиан). Граничные условия на обоих плоскостях:

t = 0, vz = 0, ¶vz/¶z = 0 при z = 0, 1

(последнее эквивалентно, виду уравнения непрерывности, условиям vx = vy = 0, при всех х, у ). Ввиду второго из уравнений (3.1) условия для vz можно заменить условиями для высших производных от t:

¶2t/¶z2 = 0, ¶3t/¶z3 – k2 ¶t/¶z = 0.

Ищем t в виде

t = f(z)j(x,y), j = e ikr, (3.3)

( где k – вектор в плоскостих, у ) и получаем для f(z) уравнение

(d2/dz2 – k2)3f + Âk2f = 0.

Общее решение этого уравнения представляет собой линейную комбинацию функций ch mz и sh mz, где

m2 = k2 - Â1/ 3k2/ 311/3

с тремя различными значениями корня. Коэффициенты этой комбинации определяются граничными условиями, приводящими к системе алгебраических уравнений, условие совместности которых дает трансцендентное уравнение, корни которого и определяют зависимости k = kn(Â), n = 1, 2, … Обратные функции Â = Â n ( k ) имеют минимум при определенных значениях k; наименьший из этих минимумов и дает значение Âкр. Оно оказывается равным 1708, причем соответствующее значение волнового числа kкр = 3,12 в единицах 1/h.

Таким образом, горизонтальный слой жидкости толщины h с направленным вниз градиентом температуры А становится неустйчивым при

gbAh3/nc>1708, (3.4)

где c - температуропроводность, n = h/r - кинематическая вязкость, h - динамическая вязкость, b = - r - 1(¶r/¶T) – температурный коэффициент расширения жидкости, r - плотность жидкости.

При Â > Âкр в жидкости возникает стационарное конвективное движение, периодическое в плоскости ху. Все пространство между плоскостями разделяются на прилегающие друг к другу одинаковые ячейки, в каждой из которых жидкость движется по замкнутым траекториям, не переходя из одной ячейки в другую. Контуры этих ячеек на граничных плоскостях образуют в них некоторую решетку. Значение kкр определяет периодичность, но не симметрию этой решетки; линеаризованные уравнения движения допускают в (3.3) любую функцию j(x, y), удовлетворяющую уравнению (D2 – k2)j = 0. Устранение этой неоднозначности в рамках линейной теории невозможно. По-видимому должна осуществляться «двухмерная» структура движения, в которой на плоскости ху имеется лишь одномерная периодичность – система параллельных полос.

В надкритической области вблизи Âкр лишь эта структура оказывается устойчивой по отношению к малым возмущениям; «трехмерные» же призматические структуры оказываются неустойчивыми. Экспериментальные результаты существенно зависят от условий опыта (в том числе от формы и размеров боковых стенок сосуда) и не однозначны. Трехмерная гексагональная структура связана, по – видимому, с влиянием поверхностного натяжения на верхней свободной поверхности, и с температурной зависимостью вязкости жидкости ( здесь вязкость n рассматривалась постоянной ).

Глава 4. Обзор статей по экспериментальному исследованию конвективной неустойчивости

4.1 Нестационарные конвективные возмущения в горизонтальном слое жидкости

Исследованию устойчивости равновесия плоскопараллельного горизонтального слоя жидкости при наличии вертикального градиента температуры посвящено очень большое число работ[10,11]. В большинстве из них устанавливаются условия, при которых наступает кризис равновесия и отыскиваются стационарные критические движения. Во многих случаях знание критических движений оказывается недостаточным, и представляет интерес изучение всего спектра возмущений, возникающих в теплостратифицированной жидкости. В настоящей работе исследуется спектр нестационарных возмущений горизонтального слоя жидкости со свободными и твердыми границами.

4.2. Численное решение одной нестационарной задачи

Подогрев снизу (a=90°). Рассмотрим теперь случай горизонтального расположения слоя при подогреве снизу[9]. Эта ориентация является в известном смысле особой. Дело в том, что при обсуждаемых условиях подогрева в этом случае возможен чисто теплопроводный режим, когда температура зависит только ог вертикальной координаты и времени, а среда остается неподвижной. Возникновение конвекции происходит тогда в результаге неустойчивости нестационарного равновесия. Эта неустойчивость развивается не сразу, а по прошествии некоторого времени, когда разность температур и ширина неустойчиво стратифицированного слоя станут достаточно большими.

g x

T = 0 a

¶T/¶y = 0 ¶T/¶y = 0

y a

L T = KT 0

Рис.4.1. Нестационарная конвекция вязкой несжимаемой жидкости в полости прямоугольного сечения

В отличие от стационарного случая, вопрос о конвективной неустойчивости нестационарного равновесия к настоящему времени изучен совершенно недостаточно. Известно лишь, что нестационарность существенно влияет на характеристики устойчивости и, в частности, на порог конвекции.

Особенности процесса разогрева иллюстрируются картами линий тока и изотерм, приведенными на рис.4.2. и рис 4.3., (l = 5;D = 0,5*106).

D = gba5K/n3, P = n/c,

где K – параметр, поределяющий темп нагрева, D – параметр, определяющий темп нагрева и интенсивность конвекции, l = L/a – относительная длина полости, а – ширина, L – длина полости, Р – число Прандтля

Из рисунков хорошо видно, как возмущения, первоначально возникшие вблизи боковых границ, развиваясь, привели к формированию (к моменту t=0,20) четырех вихрей. Теплое поле, остававшееся на начальной стадии почти теплопроводным (t=0,04; изотермы почти горизонтальны), под влиянием конвективных возмущений принимает сложньй характер, отражающий ячеистую структуру течения. На поздних стадиях процесса имеегся система восходящих и нисходящих струй, разделяющих конвектнвные вихри. В местах столкновения струй с горизонтальными границами наблюдается сильное сгущение изотерм; в этих местах достигаются экстремальные значения локальных тепловых потоков. Обращает на себя внимание «взрывной» характер развития конвекции в момент t = 0,07, очевидно, свидетельствующий о наступлении неустойчивости нестационарного равновесия.

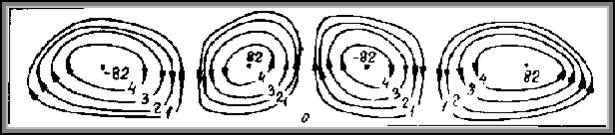
t = 0,20

t = 0,12