Второй популярный способ основан на методе градиентного спуска. При этом вначале выбираются некоторые случайные значения параметров, а затем эти значения постепенно изменяют, добиваясь наибольшей скорости роста целевой функции. Достигнув локального максимума, такой алгоритм останавливается, поэтому для поиска глобального оптимума потребуются дополнительные усилия.

Градиентные методы работают очень быстро, но не гарантируют оптимальности найденного решения. Они идеальны для применения в так называемых унимодальных задачах, где целевая функция имеет единственный локальный максимум (он же - глобальный). Легко видеть, что задача коммивояжера унимодальной не является.

Типичная практическая задача, как правило, мультимодальна и многомерна, то есть содержит много параметров. Для таких задач не существует ни одного универсального метода, который позволял бы достаточно быстро найти абсолютно точное решение.

Однако, комбинируя переборный и градиентный методы, можно надеяться получить хотя бы приближенное решение, точность которого будет возрастать при увеличении времени расчета.

Генетический алгоритм представляет собой именно такой комбинированный метод. Механизмы 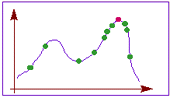скрещивания и мутации в каком-то смысле реализуют переборную часть метода, а отбор лучших решений - градиентный спуск. На рисунке показано, что такая комбинация позволяет обеспечить устойчиво хорошую эффективность генетического поиска для любых типов задач.

Итак, если на некотором множестве задана 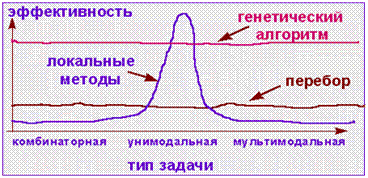сложная функция от нескольких переменных, то генетический алгоритм - это программа, которая за разумное время находит точку, где значение функции достаточно близко к максимально возможному. Выбирая приемлемое время расчета, мы получим одно из лучших решений, которые вообще возможно получить за это время.

§9. Применение генетических алгоритмов

Определим теперь понятия, соответствующие мутации и кроссинговеру в генетическом алгоритме.

Мутация — это преобразование хромосомы, случайно изменяющее одну или несколько ее позиций (генов). Наиболее распространенный вид мутаций — случайное изменение только одного из генов хромосомы.

Кроссинговер (в литературе по генетическим алгоритмам также употребляется название кроссовер или скрещивание) — это операция, при которой из двух хромосом порождается одна или несколько новых хромосом. В простейшем случае кроссинговер в генетическом алгоритме реализуется так же, как и в биологии (см. рис. 1). При этом хромосомы разрезаются в случайной точке и обмениваются частями между собой. Например, если хромосомы (1, 2, 3, 4, 5) и (0, 0, 0, 0, 0) разрезать между третьим и четвертым генами и обменять их части, то получатся потомки (1, 2, 3, 0, 0) и (0, 0, 0, 4, 5).

Блок-схема генетического алгоритма изображена на рис. 1. Вна­чале генерируется начальная популяция особей (индивидуумов), т.е. некоторый набор решений задачи. Как правило, это делается случай­ным образом. Затем мы должны смоделировать размножение внутри этой популяции. Для этого случайно отбираются несколько пар индивидуу­мов, производится скрещивание между хромосомами в каждой паре, а полученные новые хромосомы помещаются в популяцию нового поколе­ния. В генетическом алгоритме сохраняется основной принцип естест­венного отбора — чем приспособленнее индивидуум (чем больше соот­ветствующее ему значение целевой функции), тем с большей вероятно­стью он будет участвовать в скрещивании. Теперь моделируются мута­ции — в нескольких случайно выбранных особях нового поколения из­меняются некоторые гены. Затем старая популяция частично или пол­ностью уничтожается и мы переходим к рассмотрению следующего поко­ления. Популяция следующего поколения в большинстве реализаций ге­нетических алгоритмов содержит столько же особей, сколько началь­ная, но в силу отбора приспособленность в ней в среднем выше. Те­перь описанные процессы отбора, скрещивания и мутации повторяются уже для этой популяции и т. д.

В каждом следующем поколении мы будем наблюдать возникновение совершенно новых решений нашей задачи. Среди них будут как плохие, так и хорошие, но благодаря отбору число хороших решений будет возрастать. Заметим, что в природе не бывает абсолютных гарантий, и даже самый приспособленный тигр может погибнуть от ружейного вы­стрела, не оставив потомства. Имитируя эволюцию на компьютере, мы можем избегать подобных нежелательных событий и всегда сохранять жизнь лучшему из индивидуумов текущего поколения — такая методика называется “стратегией элитизма”.

Чтобы использовать генетический алгоритм для решения практи­ческих задач, необходимо рассматривать более сложные варианты вве­денных выше понятий. Поясним это на примере задачи коммивояжера для 20 городов.

В качестве индивидуумов будем рассматривать маршруты обхода. Информацию о маршруте можно записать в виде одной хромосомы — век­тора длины 20, где в первой позиции стоит номер первого города на пути следования, затем — номер второго города и т. д. Первое за­труднение возникает, когда мы пытаемся определить мутации для та­ких хромосом — стандартная операция, изменяющая только одну пози­цию вектора, недопустима, так как приводит к некорректному мар­шруту. Но можно определить мутацию как перестановку значений двух случайно выбранных генов. При таком преобразовании путь следования меняется только в двух городах.

Найденный маршрут, вероятно, не является самым оптимальным, но близок к нему по длине — как правило, генетические алгоритмы “ошибаются” не более чем на 5—10%. Этот недостаток компенсируется для комбинаторных задач относительно высокой скоростью работы — в нашем примере ответ был получен за 25 секунд. На практике генети­ческие алгоритмы нередко используют совместно с другими методами, которые позволяют повысить их точность.

Эксперименты показали, что погрешность разработанного алго­ритма не зависит от погрешности начального решения и составляет (максимальные значения) для ориентированных графов - 5%, для не­ориентированных 1%. Причем в 90% случаев алгоритм находил точное решение. Эксперименты проводились для графов с количеством вершин, меньшим 75 (где было возможным нахождение точного решения).

Список литературы

1. В.М. Бондарев, В.И. Рублинецкий, Е.Г. Качко. Основы програм­мирования, 1998 г.

2. Н. Кристофидес. Теория графов: алгоритмический подход, Мир, 1978 г.

3. Ф.А. Новиков. Дискретная математика для программистов, Пи­тер, 2001 г.

4. В.А. Носов. Комбинаторика и теория графов, МГТУ, 1999 г.

5. О. Оре. Теория графов, Наука, 1982 г.

6. www.codenet.ru

7. www.algolist.ru