d[1,5] £ d[1,2]+d[2,3]+d[3,4]+d[4,5]

Итак, если справедливо неравенство треугольника, то для каждой цепи верно, что расстояние от начала до конца цепи меньше (или равно) суммарной длины всех ребер цепи. Это обобщение расхожего убеждения, что прямая короче кривой.

Вернемся к ЗК и опишем решающий ее “деревянный” алгоритм.

1. Построим на входной сети ЗК кратчайшее остовное дерево и удвоим все его ребра. Получим граф G – связный и с вершинами, имеющими только четные степени.

2. Построим эйлеров цикл в G, начиная с вершины 1, цикл задается перечнем вершин.

3. Просмотрим перечень вершин, начиная с 1, и будем зачеркивать каждую вершину, которая повторяет уже встреченную в последовательности. Останется тур, который и является результатом алгоритма.

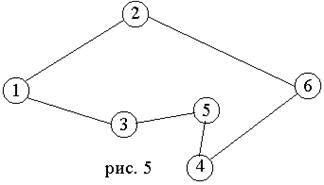Пример 1. Дана полная сеть, показанная на рис.5. Найти тур “жадным” и “деревянным” алгоритмами.

Решение.

1. “Жадный” алгоритм (иди в ближайший город из города 1) дает тур 1–(4)–3-(3)–5-(5)–4–(11)–6–(10)–2–(6)–1, где без скобок показаны номера вершин, а в скобках – длины ребер. Длина тура равна 39, тур показана на рис. 5.

2. “Деревянный” алгоритм вначале строит остовное дерево, показанное на рис. 6 штриховой линией, затем эйлеров цикл 1-2-1-3-4-3-5-6-5-3-1, затем тур 1-2-3-4-5-6-1 длиной 43, который показан сплошной линией на рис. 6.

Теорема. Погрешность “деревянного” алгоритма равна 1.

Доказательство. Возьмем минимальный тур длины fB и удалим из него максимальное ребро. Длина получившейся гамильтоновой цепи LHC меньше fB. Но эту же цепь можно рассматривать как остовное дерево, т. к. эта цепь достигает все вершины и не имеет циклов. Длина кратчайшего остовного дерева LMT меньше или равна LHC. Имеем цепочку неравенств

fB > LHC ³ LMT (9)

Но удвоенное дерево – оно же эйлеров граф – мы свели к туру посредством спрямлений, следовательно, длина полученного по алгоритму тура удовлетворяет неравенству 2LMT > fA (10)

Умножая (9) на два и соединяя с (10), получаем цепочку неравенств

2fB > 2LHC ³2LMT ³ fA (11)

Т.е. 2fB>fA, fA/fB>1+e; e=1. Теорема доказана.

Таким образом, мы доказали, что “деревянный” алгоритм ошибается менее, чем в два раза. Такие алгоритмы уже называют приблизительными, а не просто эвристическими.

§4. Метод лексикографического перебора

Известно еще несколько простых алгоритмов, гарантирующих в худшем случае e=1. Для того, чтобы найти среди них алгоритм поточнее, зайдем с другого конца и для начала опишем “brute-force enumeration” - “перебор грубой силой”, как его называют в англоязычной литературе. Понятно, что полный перебор практически применим только в задачах малого размера. Напомним, что ЗК с n городами требует при полном переборе рассмотрения (n-1)!/2 туров в симметричной задаче и (n-1)! Туров в несимметричной, а факториал, как показано в следующей таблице, растет удручающе быстро:

Чтобы проводить полный перебор в ЗК, нужно научиться (разумеется, без повторений) генерировать все перестановки заданного числа m элементов. Это можно сделать несколькими способами, но самый распространенный (т.е. приложимый для переборных алгоритмов решения других задач) – это перебор в лексикографическом порядке.

Говорят, что перестановка (a1,…,an) лексикографически предшествует перестановке (b1,…,bn), если существует k ≤ n ak < bk и для любого i > k ai = bi.

Пусть имеется некоторый алфавит и наборы символов алфавита (букв), называемые словами. Буквы в алфавите упорядочены: например, в русском алфавите порядок букв аµбµя (символ µ читается “предшествует”). Если задан порядок букв, можно упорядочить и слова. Скажем, дано слово u=(u1,u2,…,um) – состоящее из букв u1,u2,…,um — и слово v=(v1,v2,…,vb). Тогда если u1µv1, то и uµv, если же u1=v1, то сравнивают вторые буквы и т.д. Этот порядок слов и называется лексикографическим. Рассмотрим, скажем, перестановки из пяти элементов, обозначенных цифрами 1…5. Лексикографически первой перестановкой является 1-2-3-4-5, второй 1-2-3-5-4,… ,последней 5-4-3-2-1. Нужно осознать общий алгоритм преобразования любой перестановки в непосредственно следующую за ней.

Правило такое: скажем, дана перестановка 1-3-5-4-2. Нужно двигаться по перестановке справа налево, пока впервые не увидим число, меньшее, чем предыдущее (в примере это 3 после 5). Это число, Pi-1 надо увеличить, поставив вместо него какое-то число из чисел, расположенных правее, от Pi до Pn. Число большее, чем Pi-1, несомненно, найдется, так как Pi-1 < Pi. Если есть несколько больших чисел, то, очевидно, надо ставить меньшее из них. Пусть это будет Pj, j > i-1. Затем число Pi-1 и все числа от Pi до Pn, не считая Pj нужно упорядочить по возрастанию. В результате получится непосредст­венно следующая перестановка, в примере — 1-4-2-3-5. Потом получится 1-4-2-5-3 (тот же алгоритм, но упрощенный случай) и т.д.