.

Здесь p(x1,x2,…xm) – совместная плотность вероятности параметров. Интегрирование проводится по всей области D изменения параметров.

Вероятность отказов H0 к моменту очередного контроля t=t0 определяется вероятностью необнаружения дефектов размером l, превышающим критический размер l*. При продолжении эксплуатации дефекты, размеры которых не превышали предельных значений, подрастают и с течением времени могут достичь критических размеров.

Пусть к моменту времени t=t0 имеется одиночный размером l. Этот дефект системой контроля может быть обнаружен с вероятностью 1-Pa(l). Рост дефектов будем описывать уравнением (2).

(10)

где c и m- эмпирические константы, - коэффициент интенсивности напряжений, зависящий от уровня напряжений, от размеров дефекта, от свойств материала и других факторов.

Решение уравнения (10), получаемое, как правило, численно с начальным условием l(t0)=l0, зависит от ряда случайных факторов. Эта зависимость определяется случайным характером К, неопределенностью свойств материала и т.д. Обозначим вектор случайных параметров через у с компонентами у1, у2, у3…ур. Тогда решение уравнения (10) можно представить в виде

l(t)= l(y1, y2, y3…yp;t) (11)

К моменту времени t размер дефекта l(t) будет случайным с плотностью вероятности pl(l;t), где t играет роль параметра. Для нахождения распределения pl(l;t) воспользуемся правилами вычисления распределений для детерминистических функций случайных величин (3). В частности, если имеется детерминистическая функция (11), то функция распределения Fl(l;t) находится так:

(12)

где область интегрирования находится из условия l(t)= l(y1, y2, y3…yp;t)< l.

Остаточный ресурс q определяется как продолжительность эксплуатации после очередного контроля, в течение которого размер дефекта подрастает до критического значения l*. Он находится как корень уравнения

l(q)=l* (13)

Даже при фиксированных значениях l* ресурс q будет случайной величиной. Это связано со случайной зависимостью l(t). Дополнительную неопределенность вносит случайный характер критического размера l*, зависящего от случайных факторов. Плотность вероятности находится по тем же правилам, что и распределение (12).

(14)

Область интегрирования находится из условия l(t)= l(x1, x2, x3…xm;t)< l*. Вероятность отказа по критерию остаточного ресурса находится как вероятность выполнения неравенства l(t)>l*: . При известных законах распределения p1(l,t) и pl*(l*), определяемым по формулам (12) и (14), эта вероятность находится как

(15)

Формулу (15) можно упростить проинтегрировав по одной из переменных в области D[l,t,l*]:

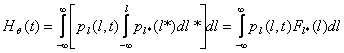(16)

Другую эквивалентную форму получим, взяв в качестве независимой переменной l*:

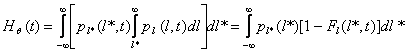(17)

Рассмотренная схема оценки вероятности отказов по критерию остаточного ресурса учитывает рост одиночного дефекта. При наличии множества начальных дефектов с различными размерами будем считать, что их рост происходит независимо. Разобьем весь интервал начальных размеров дефектов, как обнаруженных в результате контроля, так и пропущенных, на подинтервалы со средними начальными размерами lk. Обозначим через mk математическое ожидание числа дефектов, попавших в k-ый интервал. Эта величина находится через математическое ожидание kk числа обнаруженных в результате контроля дефектов в k-ом интервале и через вероятность их обнаружения Ра(lk) по формуле: .

Суммарная вероятность отказов при наличии множества дефектов находится как:

(18)

здесь через Hk(t) обозначена вероятность отказов, вычисленная по формуле (16) или (17) при начальном размере дефекта lk.

Окончательно с учетом вероятности отказов к моменту контроля t0 для вероятности отказов в момент времени t>t0 получим:

H(t)=H0+Hq(t) (19)

где вероятность H0 находится по формуле (8).

По формуле (19) можно оценит увеличение риска с течением времени эксплуатации после очередного контроля. Эта формула позволяет также оценить остаточный ресурс из условия непревышения вероятностью отказов предельного значения H*. Расчетное значение остаточного ресурса Q* находится как корень уравнения H(q)=H*.

Учет различных типов дефектов производится по формуле:

(20)

где вероятности отказов Hj(t) для каждого типа дефектов находятся согласно (19).

Для численного примера аппроксимируем функцию распределения длин дефектов F(l) и критических дефектов асимптотическими распределениями Вейбулла с параметрами l0, l*0, lc, l*c, a, a1:

(21)

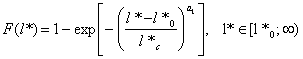(22)

Математическое ожидание числа обнаруженных дефектов аппроксимируем зависимостью с параметрам l1 и l1: .

Уравнение роста дефектов (10) перепишем в виде:

(23)

При s=const решение этого уравнения с начальным условием lk(t0)= l0k имеет вид: , где m1=m/2-1 (24)

Рассматривая параметр напряжения s как случайный с распределением Релея

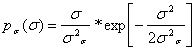(25)

Найдем распределение длин дефектов Fl(lk;t) по формуле (12), которая примет вид:

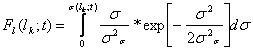(26)

где s(lk;t) – решение уравнения (24) относительно s:

(27)

После вычисления интеграла (26) получим:

(28)

Таким образом, изложенный подход к оценке вероятности отказа элементов конструкций ДЛА по результатам диагностического контроля дефектов позволяет учитывать статистическую информацию о различных типах дефектов, полученную в результате обследования, оценить остаточный ресурс после очередного диагностического обследования.

2. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ РАЗРУШЕНИЯ ПРИ ЗАДАННОМ ЗАПАСЕ ПРОЧНОСТИ.

На основании расчетов в курсе ДиПРД принимаем полученные значения n, kB1 и t.