Не следует спешить переходить к записи общего знаменателя |вод одной чертой; учащиеся часто не осознают, что производится рамена данных дробей им равными дробями с общим знаменателем.

Умножение дроби на целое число

Следующим действием изучается умножение дроби на целое число. Умножение дроби на целое число определяется так же, как умножение целых чисел.

При изучении умножения дроби на целое число необходимо установить с учащимися определение действия умножения дроби на целое число как сложения равных слагаемых, из которых каждое равно множимому; показать тождественность умножения дроби на целое увеличению дроби в несколько раз, дать определение умно­жения дроби на 1; показать рациональный прием сокращения дроби, числитель которой представляет произведение, с которым учащиеся встречаются впервые при умножении дроби на целое; научить применять это действие к задачам; рассмотреть частные случаи умножения, например, умножение дроби на число, равное знаменателю; умножение смешанного числа на целое число. Приведенный перечень задач, стоящих при изучении умножения дроби на целое число, показывает, что каждый вопрос, кажущийся простым, требует тщательного изучения и как много возникает дополнительных задач в связи с данным вопросом.

Приведем пример плана урока на эту тему,

1) Проверка домашнего задания.

2) Устные упражнения на сложение и вычитание дробей.

3) Устные примеры на деление произведения на число:

4) Сокращение дробей:

5) Повторение определения умножения на целое число:

6) Определение умножения дроби на целое число:

7) Решение задач в одно действие на умножение дроби на целое »»

число. Например: 1 м3 сосновых дров весит т. Найти вес 2м3 этих

дров (в тоннах), 7 м3.

8) Сформулировать правило умножения дроби на целое число:

чтобы умножить дробь на целое число, достаточно числитель дроби умножить на это число, оставив прежний знаменатель.

9) Решение примеров на умножение дроби на целое число:

10) Составить задачи, при решении которых требовалось бы умножить.

11) Домашнее задание.

Приведенные в этом плане устные упражнения на деление про­изведения на число и сокращение дробей имеют цель подготовить учащихся к обоснованию сокращения дробей, в числителе которых стоит произведение. Учащиеся вспоминают, как разделить произве­дение на число и при сокращении дробей ведут следующие рассуждения: чтобы сократить дробь, надо числитель и знаменатель разделить на одно и то же число; в числителе стоит произведение; чтобы произведение разделить на число, достаточно один из мно­жителей разделить на это число. Поэтому при сокращении дроби делим 10 и 25 на 5.

На следующем уроке следует предложить учащимся на несколь­ких примерах умножения дроби на целое число сравнить множимое и произведение по величине. Установить, что для дробей, как и для целых чисел, увеличить дробь в несколько раз - значит умножить ее на целое число. На основании рассмотрения примеров вида

делается вывод об изменении величины дроби с увеличением чис­лителя или уменьшением знаменателя в данное число раз и дается частный прием умножения дроби на целое число, годный для слу­чая, когда знаменатель дроби делится на данное целое число:

При изучении умножения смешанного числа на целое вначале рассматриваются два способа. Например:

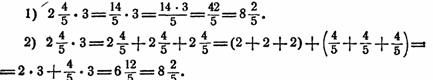
Последние рассуждения показывают справедливость распредели­тельного закона умножения относительно суммы, когда одно из слагаемых дробь. Рассматривается пример вида

и делается вывод, что при умножении смешанного числа на целое в большинстве случаев проще отдельно умножить целое и дробь на целое число.

Деление дроби на целое число

После умножения дроби на целое число следует перейти к делению целого числа и дроби на целое число, так как нахождение дроби числа, предшествующее умножению на дробь, требует деле­ния на знаменатель. На это указывается в большей части методической литературы. Определение действия деления дается как действия, обратного умножению.

Рассмотрим пример: 4 : 5.

Сначала проводятся рассуждения: чтобы разделить 4 на 5, представим мысленно каждую единицу разделенной на пять равных частей, тогда 4 единицы будут содержать 20 пятых частей, разделив 20 пятых частей на 5 получим ,что проверяется:

Мы нашли дробь, которая, будучи умноженной на 5, даст 4. Следовательно, деление произведено верно. Запишем:

Вывод. От деления целого числа на целое получается дробь, числитель которой равен делимому, а знаменатель — делителю. Об­ратно: всякую дробь можно считать за частное от деления ее чис­лителя на знаменатель.

Например, равно частному от деления 3 на 7, так как ·7=3.

Изучение деления дроби на целое число начинается с рассмотре­ния примера умножения дроби на целое число, для которого соста­вляется обратная задача. Например:

обратная задача:

требуется найти такую дробь, которая, будучи умножена на 4, даст в произведении . Такая дробь будет , запишем:

В результате рассмотрения ряда подобных примеров учащиеся приходят к выводу, что при делении дроби на целое число доста­точно числитель разделить на целое число, оставив прежний знаме­натель. После этого ставится вопрос, как поступать в том случае, когда числитель данной дроби не делится на целое число. Рассматривается второй прием умножения: , отсюда .