. (16)

Конечный продукт предприятия выразится следующим образом:

, (17)

то есть валовой продукт делится на производственное потребление предприятия как такового и поддержку частных хозяйств. Естественно предположить, что целью коллективных хозяйств будет увеличение объемов конечного продукта. Для этого разумно положить зависимость (9) линейной,

. (18)

причем при нулевом вложении труда в коллективные хозяйства помощь частным тоже должна быть нулевая и где . О множестве K следует сказать отдельно. Очевидно, что оно имеет следующий вид: K=[0, kmax]. Для определения kmax можно воспользоваться моделью, рассмотренной в предыдущей главе. При анализе случая, когда часть валового продукта идет на инвестирование производства, а остальное на поддержку частных хозяйств было получено, что расширенное воспроизводство предприятия будет иметь место при следующем соотношении экономических коэффициентов:

.

То есть n часть производственного потребления должна обязательно поступать в коллективное производство. Таким образом, максимальный отток продукта должен составить или . (19)

Тогда kmax может быть получено преобразованием выражения (18) с использованием (19):

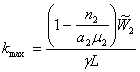или 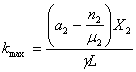. (20)

С другой стороны, можно действовать следующим образом. Предположим, что предприятие не получает никакой прибыли, однако оно должно покрыть амортизацию оборудования и заплатить зарплату своим работникам, для чего необходимо выполнение следующего неравенства:

. (21)

Где S – коэффициент оплаты труда. В этом случае в предприятии будет иметь место простое воспроизводство. Таким образом максимальный размер выделяемой помощи не должен превышать

. (22)

В результате получим:

. (23)

С учетом вышеприведенных рассуждений формула (17) перепишется следующим образом:

. (24)

Рассмотрим теперь, из каких компонентов складывается прибыль «частников». Очевидно, что это конечный продукт и заработная плата (инвестиции в данном случае принимаем равными нулю). Производственная функция будет следующей:

, (25)

при этом учтем, что производственное потребление будет удовлетворено в необходимом количестве, т. е. W1 не зависит от распределения труда. Тогда прибыль составит:

. (26)

При этом два последних слагаемых означают соответственно помощь от коллективных хозяйств и заработную плату, а S – это коэффициент оплаты труда.

Работники выбирают такое распределение трудовых ресурсов, при котором прибыль будет максимальной:

. (27)

В результате получаем следующую задачу оптимизации:

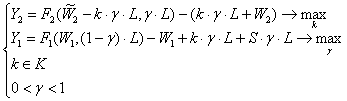(28)

Рассмотрим второе соотношение. Для достижения максимума необходимо, чтобы , и соответственно:

, (29)

что доставляет максимум функции Y1. Подставляя (29) в (28), получим:

. (30)

Для этого необходимо, чтобы .

В результате решения этого уравнения находится k=k*, оптимальное с точки зрения максимума функции Y2. Параметр g=g* вычисляется по формуле (29). Полученное решение (k*,g*) отражает состояние равновесия между подсистемами.

Также представляет интерес трансформация задачи (28) в следующий вид:

. (31)

Смысл этого выражения заключается в том, что руководитель предприятия является, как бы более "ответственным" за состояние сельского хозяйства в целом и преследует целью увеличение прибылей как коллективного, так и частных хозяйств. Коэффициент n показывает степень "важности" того или иного критерия и удовлетворяет условию 0<n<1.

6.3. Взаимодействие сельхозпредприятий и личных хозяйств для частного случая производственной функции.

Как уже было упомянуто выше, с помощью максимизации выражения (27) необходимо найти зависимость и на основании этого вычислить оптимальное значение k*.

Для этого предположим, что производственная функция предприятий имеет вид функции Кобба-Дугласа:

, (32)

где A = const > 0 – некоторый коэффициент, а .

Тогда валовой продукт частных хозяйств выражается следующим образом:

. (33)

Отсюда формула (27) примет следующий вид:

. (34)

Подсчитаем производную полученной функции. Она равна

. (35)

Для достижения максимума прибыли необходимо, чтобы

.

Таким образом

. (36)

Рассмотрим поподробнее вид полученной зависимости. При возрастании k увеличивается "поощрение" трудового вклада работника в коллективное хозяйство путем увеличения поддержки при одном и том же вкладе. Таким образом, члену кооператива становится выгоднее распределить свой трудовой потенциал в пользу кооператива. Следовательно, функция Y(k) монотонно возрастает на или . Однако величина убывает с возрастанием k так как при распределении своего труда в пользу кооператива работнику остается меньше времени для производства собственной продукции. В результате ситуация стремится к моменту когда член кооператива не сможет найти время на то чтобы воспользоваться выделенной ему поддержкой. Отсюда можно сделать вывод, что функция Y(k) вогнута. Таким образом, отметим следующие свойства зависимости g=Y(k):