Страница
2
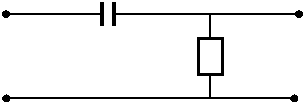 |
С
R1
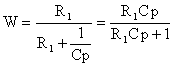
Т=1/(3 Х У)=R1C
![]()
тогда (Т-ТД)К’=Т
К’=Т/(Т-ТД)
Полученные передаточные функции корректирующего звена появляется дополнительный операционный усилитель с коэффициентом КУ /К’.
Тогда схемотехническая реализация корректирующего звена параллельного типа

![]()
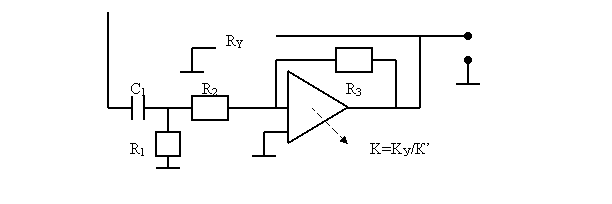
Рассчитаем:
1. R1 >> RД
RД =100 Ом
R1 =1000 Ом
2. Т=1/(3 Х У)= R1 C
1/246=1000C → C=4·10-3
3. R2 >> R1
R1 = 1000 Ом
R2 = 10000 Ом
4. K’= T/(T-TД) = -4·10-3
K=KY/K’=-50/(-4·10-3)= 12250
5. K=R3/R2; R3=K R2= 1225·105
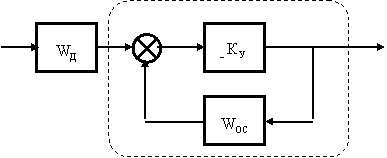
2. Корректирующая цепь c обратной связью
 |
![]() -
-![]() ;
; ![]()
Воспользуемся свойством операционного усилителя с обратными связями и сформируем на его основе соответствующие цепи обратной связи.
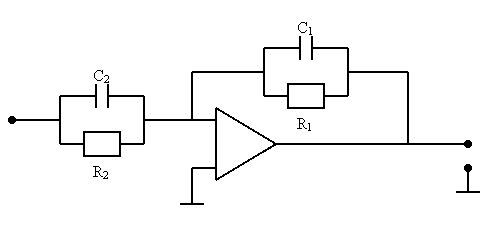
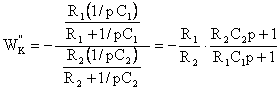
KУ=R1/R2
ТД=R2C2
Т=R1C1
Рассчитаем элементы соответствующей схемы
1. R2 >> RД
RД =100 Ом
R2 =1000 Ом
2. ТД=R2C2 → С2= ТД /R2=0,001
3. КУ= R1/R2 → R1= КУR2= 5·104
4. Т= 1/3ХУ=R1C1 → C1= 8·10-6
Таким образом наиболее эффективным способом повышения быстродействия электронного термометра является способ введения корректирующей цепи с обратной связью.
II Исследовать устойчивость типовых звеньев САУ, охваченных положительной и отрицательной обратной связью
|
W(p) |
Kp |
K/p |
K/(Tp+1) |
K/(T1p2+T2p+1) |
|
WOC |
+ 1 ; - 1 | |||
1) W(p) = Kp
WOC =1: W=WO/(1-WO)= Kp/(1- Kp)
-K>0 → K<0
WOC =-1: W=WO/(1+WO)= Kp/(1+Kp)
K>0
2) W(p) = K/p
WOC =1: ![]()
-K>0 → K<0
WOC =-1: ![]()
K>0
3) W(p) = K/(Tp+1)
WOC =1: ![]()
T>0; 1-K>0 → K<1
WOC =-1: ![]()
T>0; 1+K>0 → K>-1
4) W(p) = K/(T1p2+T2p+1)
WOC =1: ![]()
T1 >0; T2>0; 1-K>0 → K<1
WOC =-1: ![]()
T1 >0; T2>0; 1+K>0 → K>-1
III Исследовать и обеспечить в случае необходимости области устойчивости САУ, заданной структурной схемой
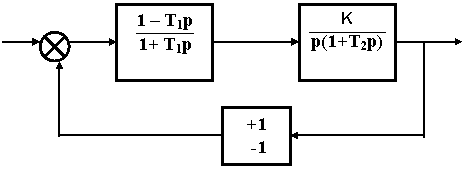 |
Т1 = 1/X;
Т2 = 1/Y;
К = X*Y,
![]()
WOC =1: ![]()
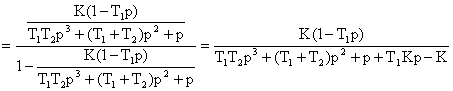
T1T2>0 1/16>0
T1+T2>0 1/8+1/2=0,625>0
1+T1K>0 1+(8*2)/8=1+2=3>0
-K>0 → K<0 8*2=16>0
(Т1+T2)(1+T1K)+T1T2>0 (1/8+1/2)(1+2)+1/16=1,9375>0
Система неустойчива параметрически, следовательно, надо изменить К в передаточной функции. Для того чтобы достаточные и необходимые условия выполнялись необходимо чтобы К удовлетворяло следующим неравенствам:
K<0
1+T1K>0 ![]()
![]()
(Т1+T2)(1+T1K)+T1T2>0 ![]()
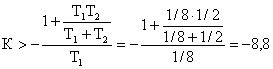
![]() -8,8 -8
-8,8 -8
0
-8<K<0
WOC =-1: ![]()
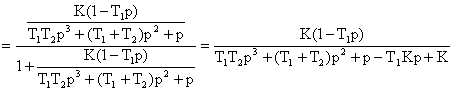
T1T2>0; 1/16>0
T1+T2>0 1/8+1/2>0
1-T1K>0 1-(8*2)/8=1-2=-1<0
K>0 8*2>0
(Т1+T2)(1-T1K)-T1T2>0 (1/8+1/2)(1-2)+1/16=-0,5625<0
Система неустойчива параметрически, следовательно, надо изменить К в передаточной функции. Для того чтобы достаточные и необходимые условия выполнялись необходимо чтобы К удовлетворяло следующим неравенствам:
K>0
1-T1K>0 ![]()
![]()
(Т1+T2)(1-T1K)-T1T2>0 ![]()
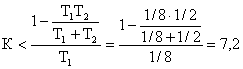
![]() 7,2 8
7,2 8
0
0<K<7,2
