Контроль качества на предприятиях-товаропроизводителях - это элемент подсистемы контроля, имеющий важное перспективное значение в обеспечении высокого качества товаров, так как он позволяет контролировать качество на всех стадиях производственного цикла, что способствует предупреждению выпуска низкого качества.

Контроль качества и ассортимента товаров должен завершаться разработкой мер по координации деятельности и корректировке программ. Только при таком подходе цель подсистемы – повышение эффективности системы управления ассортиментом и качеством товаров – будет достигнута.

Среди таких мер могут быть предусмотрены:

- разработка предложений по совершенствованию стандартов и другой научно- технической документации;

- разработка рекомендаций по повышению качества товаров, замене

товров устаревших фасонов и моделей, совершенствованию упаковки,

снижению цен, организации послепродажного обслуживания;

- разработка спецификаций новых товаров или улучшенных товаров в соответствии с требованиями потребителей.

Таким образом, подсистемой и координации завершается реализация системы управления ассортиментом и качеством товаров-(СУАК) в рамках КС УКД на основе маркетинга. Внедрение СУАК будет иметь важное значение для решения наиболее острой проблемы современного этапе развития нашей экономики – проблемы насыщения рынка высококачественными товарами в необходимом количестве и ассортименте в соответствии с запросами с запросами конкретных потребителей.

3.2. Разработка модели прогноза реализации КФХ «Людмила»

Элементы прогноза, отражающие неопределенность будущего, содержатся практически в каждом плане. Прогнозирование представляет собой процесс научного предвидения, предсказания тенденций и перспектив различных объектов и явлений на основе определения закономерностей их развития в прошлом и настоящем.

Известны различные методы прогнозирования. Однако, выбор метода, применительно к конкретным условиям, определяется природой объекта и объемом имеющейся информации о закономерностях и тенденциях его развития.

Для построения модели прогноза воспользуемся электронной таблицей Excel. Для определения объема реализации продукции возьмем данные за 1999, 2000 и 2001 года. В верхней строке указан по кварталам объём реализации продукции КФХ «Людмила» в тыс. грн. Нижняя строка представляет собой временной ряд из 12 уровней.

Таблица 3.1 — Исходные данные по объему реализации продукции КФХ «Людмилам.

Временными радами являются числовые данные наблюдений, характеризующие процессы или явления, которые постоянно изменяются во времени, а отдельные наблюдения временного ряда - уровнями этого ряда.

Временные ряды делятся на моментальные и интервальные. Моментальными рядами называются такие уровни, которые характеризуют размеры исследуемого явления в определенные даты, моменты времени.

Интервшгьными рядами называются такие уровни, которые характеризуют размеры исследуемого явления за определенные промежутки времени.

Динамику развития во времени графически можно изобразить на

рисунке 3.2.

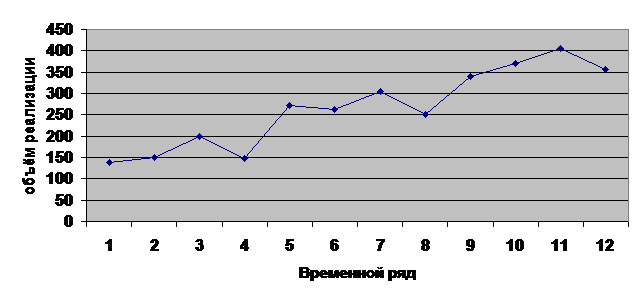Рисунок 3.2- Динамика развития во времени

Рассмотрим нелинейную модель регрессии, основываясь на выборе и обосновании типа уравнения, которое наиболее полно отразит имеющуюся связь исходных данных и построенной динамики развития.

Решение поставленной задачи возможно только при тщательном изучении всех существующих зависимостей (линейная, экспоненциальная кривая, степенная, гиперболическая, простая рациональная, логарифмическая, S-образная кривая или обратнологарифмическая).

Исследовав все выше перечисленные возможные зависимости мы определили наиболее эффективную по коэффициенту детерминированности. Ею является линейная зависимость

Расчет кривой проводится вычислением коэффициентов по известным значениям У и соответствующим значениям независимой переменной X. Линейное уравнение имеет следующий вид:

y=(a=bt) (3.1)

Алгоритмический синтаксис представляет собой:

ЛИНЕЙН((массив_у);массив_х; конст;стат) (3.2)

Перед вводом формулы с функцией ЛИНЕЙН выделяется интервал ячеек, соответствующий размеру возвышаемого им массива. Данный массив позволяет нам определить коэффициент детерминированности, основываясь на который можно провести анализ остатков, Результат этих действий выглядит следующим образом:

В соответствии с полученными результатами определился коэффициент детерминированности г2 = 0,867. Его значение показывает, что вариацию реализации (у) можно практически полностью объяснить влиянием включенного в модель временного ряда. На долю остальных, не учтенных в явном виде факторов, приходится 11,1 % вариации выходной функции.

Такую же величину нам показал и тренд линейного типа, представленный на рисунке 3.3. Для этого на графике, показывающем динамику развития во времени добавим данный тренд.