Сейчас же мы проанализируем эти формулы.

При хождении в горах никто, конечно, не вычисляет, какой рывок произойдет при срыве человека. Но для правильной оценки ситуации нужно качественно ориентироваться в ситуации и представлять от чего может зависеть величина этого рывка, когда она больше и когда меньше.

Статическая страховка без учета трения Рассмотрим случай, при котором мы осуществляем статическую страховку и не учитываем трение в верхнем карабине (как если бы мы надели на карабин ролик).

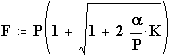, где K=(H+L)/Lo — фактор рывка.

При этом из формулы видно, что величина рывка зависит только от свойств веревки α — коэффициент жесткости веревки, от веса человека P и фактора рывка К. От того, на сколько метров человек вышел над точкой страховки, сколько точек сделал, от длины веревки и прочего рывок не зависит. Фактор рывка — это отношение глубины падения к общей длине выданной веревки. При этом сами значения глубины падения или длины веревки не влияют на рывок (то есть если глубина падения и длина веревки равны 3 метрам или они равны 30 метрам — рывок будет одинаковым). Ничего удивительного в этом нет. Действительно, при большей глубине падения в гашении рывка участвует большее количество веревки, при этом рывок оказывается одинаковым.

Величина рывка пропорциональна величинам . Например, если фактор рывка увеличился в 2 раза, то рывок увеличился в 1.4 раза (квадратный корень из 2).

Анологично — с весом.

Минимальное значение рывка в 2 раза превышает вес ( т.е. 160 кг при весе человека 80 кг). Возникает в том случае, когда просто нагружается веревка и при этом отсутствует свободная веревка. При этом К=0 — нет свободного падения вообще, веревка начинает нагружаться сразу.

Максимальное значение фактора рывка в обычно равен К=2. Такой рывок соответствует случаю, когда первый в связке не сделал ни одной точки. При этом он падает до страхующего и еще столько же вниз. К>2 могут возникнуть только в том случае, если страхующий после срыва первого успеет выбрать веревку. По этой причине (а также из соображений возможности потерять страховку) выбирать веревку после срыва ведущего категорически запрещается.

Влияние трения в верхней точке на величину рывка Рассмотрим влияние трения о карабин верхней точки, на которой происходит зависание сорвавшегося. Здесь f — коэффициент трения веревки в карабине. При очень большом трении (например, веревка застряла в карабине) ситуация эквивалентна случаю, когда рывок с фактором К=2 приходится на верхний карабин. Действительно, при этом f=1; (Lo-L1)/Lo=H/Lo=K/2; имея это в виду, выражение в скобках, указанное ниже, в которое входит f, обращается в величину K/2. Это эквивалентно ситуации, когда К=2 и нет трения.

Данное выражение в уравнении отвечает за влияние сил трения в верхней точке на величину рывка. Проанализируем его. Выражение L1/Lo может принимать значения от 0 до 1. В обычной ситуации L1/Lo=(1-К/2).

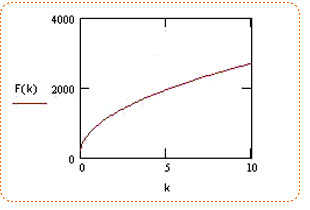
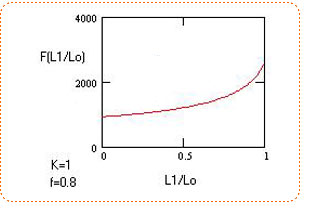
Графики зависимости F(f) и F(L1/Lo) — практически линейные. (Линейность графиков означает, что во сколько раз увеличилось трение или отношение L1/Lo, во столько раз и возрастет величина рывка). Графики приведены ниже. Имеется особенность, когда f и L1/Lo близки к 1.

Это видно на графиках. При этом величина рывка резко возрастает. Это соответствует ситуации, если при падении первого в связке резко выбрать всю веревку и трение через карабин будет высокое. При этом нагрузка придется на верхнюю точку, а на амортизацию рывка веревки, при этом, не окажется.

Графики приведены для веса 80 кг и веревке, которая при стандартном рывке UIAA имеет значение рывка 1200 кг. Такая ситуация на самом деле может присутствовать на практике и это надо иметь в виду. Например, если при одновременном движении связки происходит срыв нижнего, он может сорвать верхнего.

При одновременном падении их веревка будет двигаться в верхнем карабине. При этом первого в связке как бы затягивает в верхнюю точку и когда веревка начнет гасить его энергию падения, ее почти не останется для этой цели, рывок будет очень жестким. При таком рывке фактор рывка может оказаться гораздо выше, чем 2.

Влияние протравливания веревки на величину рывка Рассмотрим влияние протравливания веревки. При этом будем различать собственно протравливание, которое входит в понятие динамической страховки, и трение, которое возникает при движении веревки между базой и верхним карабином за счет продвижения веревки через карабины и за счет трения о неровности рельефа.

В уравнение величины рывка входит следующее выражение:

При этом участвуют две относительные величины — отношение усилия протравливания к весу человека и отношение длины протравливания к длине веревки. Как можно учитывать протравливание реально во время страховки?

Для этого выясним — как погасить рывок только протравливанием?

• Усилие протравливания
• Если усилие протравливания равно весу человека, в этом случае длина протравливания будет равна глубине падения человека.
• Если усилие протравливания больше веса человека в N раз, значит длина протравливания будет в N раз меньше, чем глубина падения. При гашении рывка только за счет протравливания сила рывка на веревку будет постоянной в течение всего периода протравливания. Этим данный прием является очень удобным и универсальным. Используя этот прием можно ходить на любой веревке (в том числе и не имеющей сертификат UIAA, даже на пеньковой веревке). Его недостаток — в сложности исполнения.
• Трение веревки о промежуточные карабины и о рельеф Этот фактор можно установить только приблизительно. Чем первому труднее выбирать веревку, тем больше такое трение. Чем больше перегибов делает веревка в карабинах, тем трение также больше. При работе в связках стараются это трение уменьшить, так как оно мешает передвижению. При этом используют оттяжки, двойную веревку и ряд других приемов. При большой величине трения рывок на верхний крюк может оказаться очень жестким (в худшем случае будет жесткий рывок с фактором рывка К=2). Итак, трение веревки действует как тормозное устройство с некоторой силой протравливания.