Содержание

Содержание

Введение

Глава 1. Основная теория сезонности временного ряда

Глава 2. Моделирование сезонности в Excel

Заключение

Литература

Введение

В процессе математического моделирования экономических явлений и объектов часто возникает необходимость оценки существующих колебательных процессов. Под сезонными колебаниями понимают более или менее устойчивую закономерность внутригодовой динамики социально-экономических явлений. Их причинами являются особенности товарного предложения, покупательского спроса, изменения затрат в зависимости от изменения климатических условий в разные временные промежутки рассматриваемого периода и т.д. Практическое значение изучения сезонных колебаний состоит в том, что получаемые при анализе рядов внутригодовой динамики количественные характеристики отображают специфику развития изучаемых явлений по месяцам (кварталам) годового цикла.

В условиях сменяемости сезонов деятельность экономических объектов сопровождается изменениями интенсивности динамики социально-экономических процессов. Это может проявляться в виде чередований подъемов и спадов различных показателей деятельности организации[1], а также приостановкой производственных процессов в определенные периоды (строительство автодорог).

Учет сезонных колебаний приводит к снижению ошибки при расчете теоретических значений показателей деятельности организации и при их прогнозировании. Использование более точных величин позволит приблизить разрабатываемую модель экономического объекта к действительности, что является одной из задач при ее создании.

Таким образом, частью задачи прогнозирования должна являться задача оценки колебательных процессов, которые могут в значительной степени влиять на получаемую картину прогнозируемого состояния объекта.

Рассмотрим часть приемов, позволяющих оценить величину сезонных колебаний. Для этого обычно используются индексы сезонности.

В литературе чаще всего рассматриваются следующие методы нахождения данных индексов:

· метод постоянной средней;

· метод переменной средней;

· метод нахождения взвешенных индексов сезонности;

· метод скользящей средней.

Рассмотрим каждый из этих методов.

1. Наиболее простым методом определения величины колебательных процессов является метод постоянной средней. Он применяется в случае отсутствия тенденции роста или убывания, когда внутригодичные изменения колеблются на протяжении изучаемого периода (ряда лет) вокруг определенного постоянного уровня [3, c.192].

2. Метод переменной средней применяется при наличии ярко выраженной основной тенденции развития[2]. В этом случае в качестве базы сравнения выступают теоретические уровни, представляющие собой своего рода "среднюю ось кривой", поскольку их расчет основан на положениях метода наименьших квадратов.

3. При изучении сезонных колебаний по данным за несколько лет их можно отделить от изменений уровней за счет наличия общей тенденции и от случайных колебаний, искажающих характер сезонной волны (индекса сезонности) в отдельные годы, путем нахождения взвешенных индексов сезонности. В данном случае индивидуальные индексы сезонности усредняются путем нахождения взвешенных средних. Весами являются средние месячные или квартальные уровни каждого года.

4. Метод скользящей средней также как и два предыдущих метода позволяет выявить и исключить общую тенденцию развития изучаемого явления. Определение общей тенденции в ряду динамики с помощью рассматриваемого метода состоит в вычислении средних величин из определенного числа членов ряда с отбрасыванием при вычислении каждой новой средней одного члена ряда слева и присоединением одного же члена ряда справа [2, c154].

Аналитик вправе использовать любой подходящий метод для определения величины колебаний. Но при достаточно серьезном моделировании экономического объекта рекомендуется воспользоваться методом нахождения взвешенных индексов сезонности или скользящей средней, причем первый из этих методов при довольно хороших результатах более удобен при расчетах.

Глава 1. Основная теория сезонности временного ряда

Основными составляющими временного ряда являются тренд и сезонная компонента. Составляющие этих рядов могут представлять собой либо тренд, либо сезонную компоненту.

Тренд является систематической компонентой временного ряда, которая может изменяться во времени. Трендом называют неслучайную функцию, которая формируется под действием общих или долговременных тенденций, влияющих на временной ряд. Примером тенденции может выступать, например, фактор роста исследуемого рынка.

Автоматического способа обнаружения трендов во временных рядах не существует. Но если временной ряд включает монотонный тренд[3], анализировать временной ряд в большинстве случаев нетрудно.

Существует большое разнообразие постановок задач прогнозирования, которое можно подразделить на две группы: прогнозирование односерийных рядов и прогнозирование мультисерийных, или взаимовлияющих, рядов.

• Группа прогнозирование односерийных рядов включает задачи построения прогноза одной переменной по ретроспективным данным только этой переменной, без учета влияния других переменных и факторов.
• Группа прогнозирования мультисерийных, или взаимовлияющих, рядов включает задачи анализа, где необходимо учитывать взаимовлияющие факторы на одну или несколько переменных [6, c.312].

Кроме деления на классы по односерийности и многосерийности, ряды также бывают сезонными и несезонными. Последнее деление подразумевает наличие или отсутствие у временного ряда такой составляющей как сезонность, т.е. включение сезонной компоненты.

Сезонная составляющая временного ряда является периодически повторяющейся компонентой временного ряда. Свойство сезонности означает, что через примерно равные промежутки времени форма кривой, которая описывает поведение зависимой переменной, повторяет свои характерные очертания. Свойство сезонности важно при определении количества ретроспективных данных, которые будут использоваться для прогнозирования.

Рассмотрим простой пример. На рисунке 1 приведен фрагмент ряда, который иллюстрирует поведение переменной "объемы продажи товара Х" за период, составляющий один месяц. При изучении кривой, приведенной на рисунке, аналитик не может сделать предположений относительно повторяемости формы кривой через равные промежутки времени.

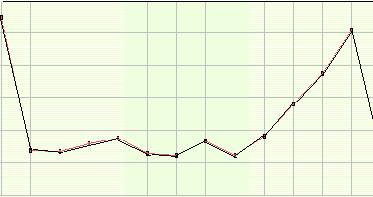
Рис. 1. Фрагмент временного ряда за сезонный период

Однако при рассмотрении более продолжительного ряда (за 12 месяцев), изображенного на рисунке 2 можно увидеть явное наличие сезонной компоненты. Следовательно, о сезонности продаж можно говорить только, когда рассматриваются данные за несколько месяцев.