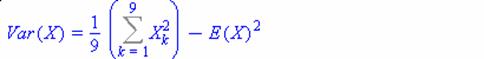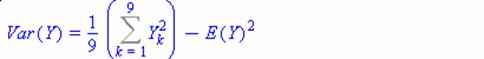История развития семейной структуры

Рефераты >> Статистика >> История развития семейной структуры

Следовательно, регрессия значима

Проверим значимость коэффициента корреляции

Поэтому выборочный коэффициент корреляции значимо отличается от нуля.

Прогноз на 2007

Точечный прогноз для

Прогноз на 2008

Точечный прогноз для

Построенная регрессия обладает хорошими прогнозными свойствами. Согласно ей, убыль населения будет происходить и в дальнейшем.

Население в трудоспособном возрасте

Приведем массив данных

Построение регрессии

Для регрессии вида

найдем коэффициенты по формулам

Вычислим

Тогда

Откуда

Тогда линейная регрессия будет иметь вид

Смысл коэффициента beta заключается в том, что при изменении значения X на 1 единицу Y меняется на 0,66 единиц

Нарисуем точки и регрессию:

Подсчитаем оценку дисперсии ошибки, т.е.

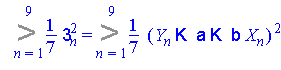
Среднее X

Найдем оценки дисперсий коэффициентов регрессии

по формулам

Получим

Эластичность

Подсчитаем функцию эластичности по формуле

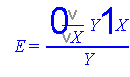
В нашем случае

или

Значение эластичности в средней точке

Показывает, что при изменении X на 1% Y меняется на 0,058 процентов.

Изучение качества регрессии

Доверительные интервалы для оцененных параметров

уровень доверия

Количество степеней свободы 7

Критическое значение статистики Стьюдента

Доверительный интервал для beta

равен

Не можем на данном уровне значимости принять гипотезу beta=0 т.к. не попадает в доверительный интервал.

Доверительный интервал для alpha

равен

Мы не можем на данном уровне значимости принять гипотезу alpha=0 т.к. не попадает в доверительный интервал.

Критерий Фишера значимости всей регрессии

Коэффициент корреляции

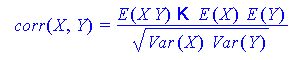
где