Дисперсионный анализ дает возможность установить влияние группировочного признака и влияние случайных величин на результативный признак. При этом общая дисперсия результативного признака расчленяется на факторную и остаточную (или случайную) ; факторную дисперсию сравнивают со случайной с учетом степеней свободы. Число степеней свободы: для общей дисперсии – число значений варьирующего результативного признака без одного (n–1), для факторной дисперсии – число групп без одной (I–1), для случайной дисперсии – число значений результативного признака без числа групп (n–1). Обозначив сумму квадратов отклонений через D2, получим дисперсию на одну степень свободы:

– общую ; (24)

– факторную ; (25)

– случайную . (26)

Общая дисперсия определяется по формуле . (27)

Далее вся совокупность делится на однородные группы. Для каждой группы рассчитывают среднюю и дисперсию. В результате получают внутригрупповую и межгрупповую дисперсии. Общая дисперсия показывает влияние всех условий (факторов) на вариацию признака Внутригрупповая (случайная) дисперсия показывает влияние случайных, не учитываемых условий (факторов) на вариацию признака, то есть зависит от группировочного признака. Она представляет собой среднюю из частных (групповых) дисперсий () и рассчитывается по формуле:

, (28)

а частные (групповые) дисперсии рассчитываются следующим образом:

. (29)

Межгрупповая дисперсия характеризует вариацию признака под влиянием определяющих условий, связанных с группировочным признаком. Она представляет собой средний квадрат отклонения групповых средних от общей средней и вычисляется по формуле:

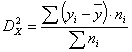. (30)

Оценка достоверности влияния факторного признака на результативный производится с помощью рассчитанного значения F-критерия (критерия Фишера). Критерий Фишера есть отношение факторной и случайной дисперсий, рассчитанных на одну степень свободы:

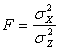. (31)

Величина рассчитанного критерия сравнивается с его табличным значением, установленным для 1- и 5-процентного уровня значимости, если значение FФАКТ < FТАБЛ.

Регрессионный анализ позволяет определить меру интенсивности направленного влияния факторов при формировании уровня производительности труда в конкретных условиях места и времени. Вначале устанавливается тип и вид функции уравнения связи. Конкретное выражение формы связи зависит от характера объективно существующей зависимости исследуемых явлений, т.е. определяется материальной природой объекта.

Количественная определенность параметров уравнения связи устанавливается чаще всего по методу наименьших квадратов. При этом находятся такие численные значения коэффициентов при факторных признаках в уравнении регрессии, при которых сумма квадратов отклонений эмпирических значений результативного показателя от аналогичных им величин, рассчитанных по теоретическому уравнению регрессии, давала бы минимальную величину.

Корреляционный анализ дает возможность измерить взаимосвязь (тесноту связи) факторного и результативного признаков. Для этого предварительно устанавливается для каждой группы центр интервала по размеру производительности труда, а затем рассчитывается коэффициент корреляции по формуле:

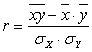, (32)

где ; ; ;

;

;

X – группировочный (факторный) признак;

Y – результативный признак;

N – численность совокупности;

M – математическое ожидание;

h – среднее квадратичное отклонение.

Вычисление коэффициента корреляции является наиболее точным, если оно проводится по всему массиву не сгруппированных первичных данных.

Список использованной литературы

1. Елисеева И.И., Юзбашева М.М. Общая теория статистики, – М.,1995 г.

2. Статистика промышленности , под ред. Адамова В.Е., – М., 1987 г.

3. Савицкая Г. В. Анализ хозяйственной деятельности предприятия. – М.: Инфра‑М, 2001

4. Шеремет А.Д., Сайфулин Р.С. Методика финансового анализа – М.: ИНФРА‑М, 1999.

5. Анализ трудовых показателей: Учеб. Пособие для вузов / А.В. Никитин, Н.А. Кольцов, И.А. Самарина и др.; Под ред. П.Ф. Петроченко. – М.: Экономика, 1989.