Реализацией (траекторией, выборочной функцией) случайной функции X(t) называют неслучайную функцию аргумента t, равной которой может оказаться случайная функция в результате испытания. Таким образом, если в опыте наблюдают случайную функцию, то в действительности наблюдают одну из возможных ее реализаций; очевидно, при повторении опыта будет наблюдаться другая реализация.

Реализации функции X(t) обозначают строчными буквами x1(t), x2(t) и т.д., где индекс указывает номер испытания. Например, если X(t)=U sin t, где U – непрерывная случайная величина, которая в первом испытании приняла возможное значение u1=3, а во втором испытании u2=4.6, то реализациями X(t) являются соответственно неслучайные функции x1(t)=3 sin t и x2(t)=4.6 sin t.

Итак, случайную функцию можно рассматривать как совокупность ее возможных реализаций.

Если t – время, то случайную функцию называют случайным процессом.

Математическое ожидание случайной функции:

неслучайная функция, значение которой при каждом фиксированном значении аргумента t равно математическому ожиданию сечения, соответствующего этому же фиксированному значению аргумента. Геометрически математическое ожидание случайной функции можно истолковать как «среднюю кривую», около которой расположены другие кривые – реализации; при фиксированном значении аргумента математическое ожидание есть среднее значение сечения («средняя ордината»), вокруг которого расположены его возможные значения (ординаты).

Центрированной случайной функцией называют разность между случайной функцией и ее математическим ожиданием:

Рассмотрим случайную функцию X(t). При двух фиксированных значениях аргумента, например при t=t1 и t=t2 получим два сечения – систему случайных величин X(t1) и X(t2) с корреляционной функцией

Стационарной случайной функцией называется такая случайная функция, математическое ожидание которой сохраняет одно и то же значение при всех значениях аргумента t и корреляционные функции зависят только от разности аргументов t2-t1:

Спектральной плотностью стационарной случайной функции X(t) называют функцию sx(w), которая связана с корреляционной функцией взаимно-обратными преобразованиями Фурье:

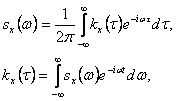
Белый шум – стационарная случайная функция, спектральная плотность которой постоянна: sx(w) = s = const. Корреляционная функция белого шума:

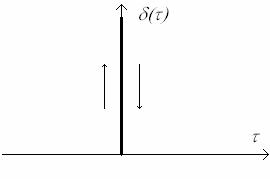
. Здесь 2ps – коэффициент пропорциональности, называемый интенсивностью белого шума; d(t) – дельта-функция (математическая абстракция):

Название «белый шум» объясняется некоторой аналогией с белым светом: белый свет представляет собой сумму всех спектральных составляющих, имеющих одну и ту же интенсивность. Белый шум представляет собой сумму гармонических колебаний всех частот, имеющих одну и ту же дисперсию амплитуды. Белый шум является к тому же чисто случайной функцией – т.е. для него x(t1), x(t2),… взаимно независимы для любого конечного множества значений аргумента t1, t2, … .

Библиография:

1. Колемсов О.В., Старовертов В.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. – М., Высшая школа, 1991г.

2. Яковлев Г.И. Алгебра и начала анализа. чII.- М., Науки, 1988г.

3. Прохоров Ю.В., Розаков Ю.А. Теория вероятностей. – М., Наука, 1987г.

4. Гончаров Р.В., Любимов М.Ф. Информатика. Задачи, примеры и контрольные задания. - Ростов-на-Дону; РГЭА, 1999.

5. Гончаров Р.В., Любимов М.Ф., Савельева Н.Г. Информатика. Компьютерные системы и сети. Учебное пособие. - Ростов-на-Дону; РГЭА, 1998.

6. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1977.

7. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1977.

8. Коршунов Ю.М. Математические основы кибернетики. М.: Энергоатомиздат, 1987.