,

но при не существует, поэтому рассмотрим случай когда n=+1 :

(т.к. см. разложение выше)

и случай когда n=-1:

(т.к. )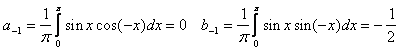

И вообще комплексная форма:

или

или

Цифровые фильтры

Как правило, цифровой фильтр ЦФ является специализирован­ной ЭВМ. Иногда в качестве цифрового фильтра используется универсальная ЭВМ.

Рассмотрим принцип работы ЦФ. На его вход подается сигнал х(пТ) • последовательность числовых значений, следующих с интервалом Т. При поступлении каждого очередного числа х(пТ) ЦФ производит расчет по соответствующему алгоритму и на вы­ходе появляется выходное число у(пТ). В общем случае число у(пТ) является функцией ряда предыдущих значений как вход­ных х^ так и выходных у чисел:

у (nT) = f [х (п Т), х (п Т— Т), х(пТ — 2Т), .,

На выходе фильтра вырабатывается последовательность чисел у(пТ), следующих с интервалом Т. Таким образом, тактовый ин­тервал Т является общим для входных и выходных чисел.

Остановимся на основных структурных схемах линейных ЦФ.

Цифровые фильтры делятся на два большие класса: нерекур­сивные и рекурсивные. В нерекурсивных фильтрах отклик зависит только от значений входной последовательности у(пТ) = Р[х(пТ),х-(пТ — Т),.,.].

В рекурсивных фильтрах отклик зависит как от значений вход­ной последовательности, так и от предшествующих значений вы­ходной последовательности

y(nT)=f{x(nT),x(nT—T), .,у(пТ—Т),у(пТ—2Т), .}.

Нерекурсивный цифровой фильтр. На рис. 10.19 изображена структурная схема нерекурсивного цифрового фильтра, обрабаты­вающего сигнал в соответствии с алгоритмом

+ . + Ьмх(пТ—МТ).

На схеме обозначены: z~l - - регистры сдвига, осуществляющие сдвиг цифровой последовательности на один такт Т\ bi — умно­жители на числа be, Е - сумматор.

Нерекурсивный ЦФ может быть практически осуществлен, если заданная импульсная характеристика содержит сравнитель­но небольшое число членов, т. е. быстро убывает с ростом п. В противном случае для получения заданной импульсной характе­ристики потребуется очень много ячеек памяти.

Рекурсивный цифровой фильтр. Рекурсивный ЦФ характери­зуется тем, что выходное число у(пТ) зависит от ряда поступив­ших на вход чисел и от предшествующих выходных чисел

(1)

Запишем алгоритм (1) ЦФ JV-ro порядка в виде разност­ного уравнения соответствующего порядка

y(nT)-aly(nT—T) — .—aNy(nT-NT) = bQx(nT) + .+ Ьмх(пТ—МТ),

которое эквивалентно линейному дифференциальному уравнению Лт-го порядка для аналогового фильтра.

Правая часть уравнения (10.65) описывает нерекурсивную, ле­вая - - рекурсивную части ЦФ. Коэффициенты ао, а\, ., un, b\> &2, ., Ьм определяются значениями элементов схемы фильтра.

Структурная схема рекурсивного фильтра, осуществляющего обработку в соответствии с алгоритмом (1), изображена на рис. 2.

Определим системную функцию Н (z) цифрового фильтра. Для этого применим к уравнению (10.65) г-преобразование и теорему смещения

(3)

Выражение (3) связывает системную функцию фильтра со зна­чениями его элементов. По известной (заданной) системной функ­ции Н (z) может быть определена структура .и значения коэффи­циентов ЦФ.

Основным достоинством рекурсивных фильтров является со­кращение числа элементов структурной схемы по сравне­нию с числом элементов в не­рекурсивных фильтрах. Благо­даря этому они позволяют реа­лизовать медленно.затухающие х(пт-т) импульсные характеристики.

Недостатком рекурсивных фильтров являются большие ошибки округления, нежели в нерекурсивных фильтрах.

Рекурсивные фильтры позволяют реализовать любые алго­ритмы типа (1), т, е. получить весьма разнообразные частот­ные характеристики при соблюдении следующих условий:

а) все полюса системной функции Н (z) должны лежать на 2-плоскости внутри окружности радиуса ]z| = l, т. е. система дол­ жна быть устойчивой;

б) ошибки округления не должны нарастать в такой степени, чтобы нарушать нормальную работу фильтра

рекурсивный цифровой фильтр. Канонический рекурсивный ЦФ является результатом модификации структурной' схемы на рис. 2, реализующей фильтр с системной функцией вида (3).