1.2 Взгляд на Т.С.В. из ХХ века

Современное состояние науки также не согласуется с предположением о тепловой смерти Вселенной. Прежде всего, этот вывод имеет отношение к изолированной системе и не ясно, почему Вселенную можно относить к таким системам.

Во Вселенной действует поле тяготения, которое не принималось Больцманом во внимание, а оно ответственно за появление Звезд и Галактик: силы тяготения могут привести к образованию структуры из хаоса, могут породить Звезды из Космической пыли. Интересно дальнейшее развитие термодинамики и с ней на идею о Т. С.В. На протяжении XIX века были сформулированы основные положения (начала) термодинамики изолированных систем. В первой половине XX века термодинамика развивалась в основном не вглубь, а вширь, возникали различные ее разделы: техническая, химическая, физическая, биологическая и т.д. термодинамики. Только в сороковых годах появились работы по термодинамике открытых систем вблизи точки равновесия, а в восьмидесятых годах возникла синергетика. Последнюю можно трактовать как термодинамику открытых систем вдали от точки равновесия. Итак, современное естествознание отвергает концепцию "тепловой смерти" применительно к Вселенной в целом. Дело в том, что Клаузиус прибегнул в своих рассуждениях к следующим экстраполяциям:

1. Вселенная рассматривается как замкнутая система.

2. Эволюция мира может быть описана как смена его состояний.

тепловая смерть вселенная энтропия

Для мира как целого состояния с максимальной энтропией это имеет смысл, как и для любой конечной системы. Но сама по себе правомочность этих экстраполяций весьма сомнительна, хотя связанные с ними проблемы представляют трудность и для современной физической науки.

2. Закон возрастания энтропии

2.1 Вывод закона возрастания энтропии

Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 1.

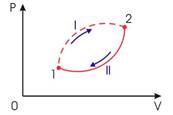
Рис.1. Необратимый круговой термодинамический процесс

Пусть процесс будет необратимым, а процесс - обратимым. Тогда неравенство Клаузиуса для этого случая примет вид

Так как процесс является обратимым, для него можно воспользоваться соотношением (3.53) , которое дает

Подстановка этой формулы в неравенство (3.55) позволяет получить выражение

Сравнение выражений (3.53) и (3.57) позволяет записать следующее неравенство

в котором знак равенства имеет место в случае, если процесс является обратимым, а знак больше, если процесс - необратимый.

Неравенство (3.58) может быть также записано и в дифференциальной форме

Если рассмотреть адиабатически изолированную термодинамическую систему, для которой , то выражение (3.59) примет вид

или в интегральной форме

2.2 Возможность энтропии во Вселенной

В адиабтически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс. Записанное утверждение является ещё одной формулировкой второго начала термодинамики. Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия. Необходимо отметить, что если система не является изолированной, то в ней возможно уменьшение энтропии. Примером такой системы может служить, например, обычный холодильник, внутри которого возможно уменьшение энтропии. Но для таких открытых систем это локальное понижение энтропии всегда компенсируется возрастанием энтропии в окружающей среде, которое превосходит локальное ее уменьшение.

С законом возрастания энтропии непосредственно связан парадокс, сформулированный в 1852 году Томсоном (лордом Кельвином) и названый им гипотезой тепловой смерти Вселенной. Подробный анализ этой гипотезы был выполнен Клаузиусом, который считал правомерным распространение на всю Вселенную закона возрастания энтропии. Действительно, если рассмотреть Вселенную как адиабатически изолированную термодинамическую систему, то, учитывая ее бесконечный возраст, на основании закона возрастания энтропии можно сделать вывод о достижении ею максимума энтропии, то есть состояния термодинамического равновесия. Но в реально окружающей нас Вселенной этого не наблюдается.
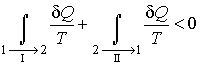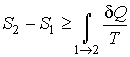