E1 < E2 < E3 < . < En-1 < En < En+1 < . < Ei (1)

где En тем больше, чем больше n, но все En меньше, чем Ei. Ei здесь - значение энергии ионизации одиночного атома. Для случая водорода Ei = 13,53 eV. Разница между двумя соседними значениями энергии в этом неравенстве становится с ростом n всё меньше и меньше.

Представленные в ряду (1) значения энергий En являются энергиями поглощения. Эти порции энергии нужны электронам, чтобы переместиться к свободному протону. Так как спектр поглощения, как принято считать, идентичен спектру излучения, то можно предположить, что описанный выше ряд энергетических значений (1) аналогичен серии Лимана в спектре излучения водорода:

Em-1 = hcRy(1-1/m2) где m = 2,3,4 . (2)

Здесь h – постоянная Планка, c – скорость света, Ry – постоянная Ридберга.

Сравнение полученного спектра со спектром Лимана

Чтобы подтвердить это предположение соответствующим расчётом, необходимо было бы знать зависимость F(r) силы взаимодействия F между электроном и протоном в зависимости от расстояния r между ними, при расстояниях r меньше одного микрона. По принятой выше гипотезе эта зависимость должна выглядеть примерно так, как показано на рис. 2. Сила притяжения сперва растёт (примерно обратно пропорционально квадрату расстояния) по мере уменьшения расстояния, а затем быстро уменьшается до нуля и превращается в силу отталкивания, которая растёт ещё быстрей.

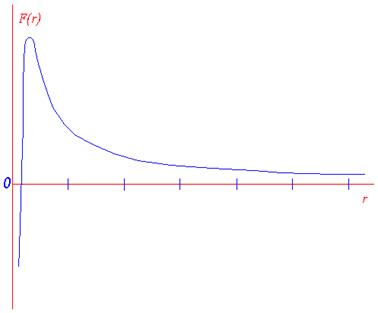
Рис. 2

Энергия, которую электрон получает в поле одиночного протона, можно выразить в соответствии с законом Кулона через интеграл C(1/ro - 1/r), или, что тоже самое, посредством выражения

C1(1 - r0/r) (3).

Нильс Бор в своё время сравнил выражение (3) с выражением (2) для частот серии Лимана, идентичное выражению C2 (1 - 1/n2), и понял, что отсюда можно получить

1/r ~ 1/n2 (4),

где значок (~) обозначает “пропорционально”. Если в последнем выражении текущее значение r заменить на дискретное rn, то из (4) немедленно следует: rn ~ n2. Полученный результат надо было после этого только истолковать. У любого человека r ассоциируется прежде всего с радиусом окружности. Орбита электрона в виде окружности уже была известна из толкования результата своих экспериментов Резерфордом (бывшего научного руководителя Нильса Бора). Бор сделал из произвольной окружности бесконечную серию “разрешённых”. Физического обоснования своего “поступка” он не дал. Это было чисто математическое толкование по принципу: “ведь совпадает с результатом”. Точно также “совпадали с результатом” расчёты астрономов по системе Птолемея – без понимания существа происходящего. (Кто-нибудь скажет: “А чем это плохо? Главное – умели рассчитать!” Разумеется, но, возможно, тогда не возникло бы понятия о силе тяжести. Не появились бы не только аппараты, которые тяжелее воздуха – самолёты и ракеты, но и те, что легче. Да, наверное, и многое другое – не появилось бы.)

Нильс Бор считал, что характерный спектр излучения (водорода) происходит от движений электрона в поле одиночного протона. Поэтому происхождение бесконечной серии частот излучения водорода можно было объяснить только за счёт идеи “сложного устройства” атома. В среде частично ионизированного газа (водорода) гораздо более естественно ожидать движение электрона от одного протона к другому. Это позволяет отказаться от идеи сложного устройства атома (атом водорода состоит только из двух элементарных, т.е. простых частиц!) Сложный спектр может получаться за счёт относительно сложного (по сравнению с атомом) устройства сави. Нейтральный атом из одного из слоёв сави “теряет” свой электрон, его принимает ион (свободный протон) в центре сави. Так как слои нейтральных атомов находятся на различном, ступенчато изменяющемся расстоянии от иона в центре сави, то ступенчато меняется и необходимая для ионизации обмена (отрыва электрона от своего протона в поле другого протона) энергия. Этими расстояниями определяется порционирование энергии поглощения. Чисто схематически электрон всегда движется между двумя протонами (рис. 3), от положения равновесия вблизи одного протона к положению равновесия вблизи другого. То есть математически мы будем иметь дело с наложением двух поворотно симметричных функций, силовым воздействием двух протонов на один электрон. Силовое поле, в котором при этом движется электрон, схематически показано на рис. 4. Вблизи своего протона в точке 1 электрон получает импульс (порцию энергии). В идеальном случае его хватает как раз на то, чтобы достигнуть точку ri посредине между двумя протонами, где силовое воздействие равно нулю. В этой точке, израсходовав всю энергию, скорость электрона тоже становится (практически) равной нулю. Дальше электрон движется в симметрично равном силовом поле к другому протону и, достигнув положения равновесия (точка 2), имеет ту же самую энергию и тот же самый импульс, который имел по выходе из точки 1. Так как электрон в точке 2 имеет некоторый импульс, т.е. скорость, то он в точке 2 не сможет остановиться и проскочит её. Начиная с точки 2 на электрон будет действовать отталкивающая сила, поэтому он будет вскоре остановлен и отброшен обратно. После того, как он снова минует положение равновесия, он будет снова притягиваться в сторону точки 2 и т.д. При этом колебательном движении электрон будет излучать энергию. После определённого числа колебаний, излучив всю полученную энергию, электрон займёт положение равновесия в точке 2. Таким образом, расстоянием между двумя протонами, обменивающимися электроном, порционируется не только энергия поглощения, но и излучения.

Рис. 3

Этим показана возможная физическая основа возникновения спектров поглощения и излучения. Кроме того, следует ещё показать, в соответствии с какими зависимостями должны изменяться кривые на рис. 2 и 4, чтобы получить соответствие полученной последовательности значений энергии (1) серии Лимана. Если в сави расстояние между слоями нейтральных атомов всегда одно и то же, тогда изменение функции S(n), представляющей последовательность площадей Si на рис. 4, будет пропорционально изменению интеграла от функции 1/r3, взятому в пределах от r0 до rn.

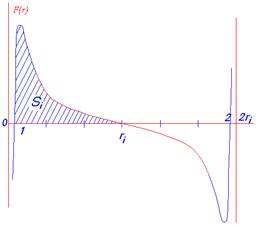
Рис. 4

Вместо выражения (3), применённого Бором, следует взять выражение для площади Si на рис. 4:

Sn = C3(1 - r02/rn2) (5)

Тогда сравненивая (5) с (2), можно получить результат rn2 ~ n2, или, что то же самое:

r ~ n (6)

Этот результат соответствует строению сави по рис. 1. И здесь тоже r будет означать радиус, но не орбиты электрона, а сферического слоя сави. Следовательно, можно получить полное соответствие со спектральными частотами серии Лимана без утверждения, что атомы похожи на миниатюрные планетные системы. Природа не повторяет сама себя.

Возможно, что расстояние между сферическими слоями нейтральных атомов сави в действительности не остаётся постоянным, что оно постепенно растёт по мере увеличения номера слоя. Тогда выражение для площади Si (рис. 4) будет более сложным. Естественно, что сави не может иметь бесконечное число сферических слоёв. Несколько десятков слоёв являются уже более, чем достаточными, чтобы получить необходимый спектр.