Гипотеза литосферных плит основана на их способности скользить по поверхности астеносферы (расплавленным глубинным породам), чем поверхность Земли приводится в состояние, близкое к гидростатическому равновесию. Эта теория получила признание в 60-е гг. XX в. Считается, что верхний слой коры состоит из 15 жестких плит, из них 50 % — крупные (до 1000 км), которые плавают на горячем, пластичном слое мантии Земли по поверхности астеносферы. При этом плиты могут сталкиваться, погружаться друг под друга и надвигаться одна на другую. Вместе с плитами могут перемещаться и континенты. Эту гипотезу называют гипотезой новой глобальной тектоники, поскольку впервые попытались объяснить развитие Земли с помощью данных, полученных при изучении развития континентов и океанов. Литосферу моделируют системой плит, перемещающихся относительно друг друга со скоростями несколько сантиметров в год. Так, Гималаи, Памир и Тянь-Шань — результат надвигания одной плиты на другую.

При росте плит расширяется океаническая котловина, магма поднимается, застывает и образует вдоль подводного хребта океаническую кору. При замедленном процессе сокращается протяженность спрединговых центров. В настоящее время длина такой системы около 56 тыс. км, а скорости развития порядка 5 см/год (в Атлантике — почти вдвое ниже, в Тихом океане — в 3 раза выше). Умножая среднюю скорость роста на длину спрединговых центров, получим скорость формирования коры — 2,8 км2/год. Средняя площадь океанов — 310 млн км2, т.е. они сформировались за 110 млн. лет. Средством проверки гипотезы тектоники плит служила программа бурения с судна «Гломар Челленджер». Результаты бурения дна подтверждают, что океаны более «молоды», чем считали ранее. Возраст западной части Тихого океана — до 180 млн лет, т.е. за последние 2 млрд лет могли возникнуть и исчезнуть до 20 океанов. Если дно и континент принадлежат к одной и той же плите, то континент перемещается вместе с ней. Океаническая кора может погрузиться под континент, присоединяясь к мантии (субдукция). Кора поднимается на хребте, перемещается поперек котловины и погружается вдоль желоба, отделяющего зону субдукции. Породы охлаждаются в океане, растекаются по оси хребта и в стороны от него, и кора постепенно погружается. Некоторые горы на океаническом плато настолько велики, что поднимаются, как острова. Подводные горы чаще всего базальтовые и появляются из «горячих точек», расположенных под плитой. Если плита скользит по магме, возникает целая цепь быстро растущих вулканов, как на Гавайских островах. Скопления минерального сырья по всем границам плит подтверждает существование таких процессов.

4. Как осуществляется математическое моделирование биологической эволюции

Математическое моделирование как научное направление еще очень молодо, и, судя по всему, его эволюция в рамках компьютерно-технологических сдвигов продолжается .

Построение моделей представляет собой "применение фундаментальных законов природы, вариационных принципов, аналогий, иерархических цепочек", а процесс построения модели включает в себя следующие этапы:

«Cловесно-смысловое описание объекта или явления" ("формулировка предмодели»);

«Завершение идеализации объекта» и упрощение описания;

Переход «к выбору или формулировке закона (вариационного принципа, аналогии и т.п.)» и его записи в математической форме;

«Завершает формулировку модели ее «оснащение» (задание начального состояния и параметров объекта). Этот этап особенно важен, поскольку:

«И, наконец, формулируется цель исследования модели (найти закон преломления света, достичь понимания закономерностей изменения популяции, определить требования к конструкции ракеты, запускающей спутник, и т.д.)»;

Модель изучается всеми доступными методами (в том числе с применением различных подходов и вычислительных методов);

В результате исследования модели достигается поставленная цель. При этом "должна быть установлена всеми возможными способами (сравнением с практикой, сопоставлением с другими подходами) ее адекватность - соответствие объекту и сформулированным предположениям".

Последовательность этапов моделирования, соответствующая этому разбиению, представлена нами на рис. 1.

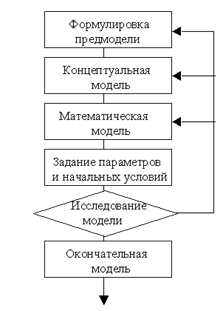
Рис.1

Плодотворность методологии математического моделирования при решении разнообразных задач за прошедшие годы была неоднократно подтверждена многочисленными примерами из области механики, термодинамики, биологии, экономики и социальных наук.

Демографическим проблемы, связанным со старением и плохим воспроизводством населения, в последнее время уделяется все больше внимания . Исследования на человеческом материале в силу целого ряда обстоятельств часто не позволяют получить убедительных результатов. Проблема связи старения с генетическими (наследственными) факторами, условиями жизни и окружающей средой относятся к числу таких проблем. Эксперименты на животных с более простой генетической и физиологической организацией и с коротким жизненным циклом позволяют глубже понять общебиологические основы старения и, в принципе, начать разработку мер по продлению жизни и предотвращению преждевременного старения у человека. Стандартные эксперименты чаще всего ставятся на популяциях плодовитых и короткоживущих насекомых (плодовая мушка Drosophila и средиземноморская мушка Ceratitis Capitata). Исследование последней имеет и самостоятельное прикладное значение, поскольку в ряде эта мушка является наиболее распространенным вредителем фруктовых плантаций, и уже около десяти лет выращивается в промышленных масштабах в Мексике в рамках программ биологической защиты урожая.

«Академический» этап моделирования старения представлен классическими популяционно-генетическими моделями Фишера, физиологическими моделями, моделями "теории надежности" и термодинамическими моделями. Переход к активным компьютерным методам исследования связан с переходом к методам Монте-Карло. Следуя давней традиции , физики с энтузиазмом берутся за решение кардинальных вопросов жизни, в данном случае за разработку моделей старения. Наиболее известна изящная bit-string модель бразильского физика Пенны (представляющая геном в виде строки двоичных сигналов). Однако, как и в случае анализа "жизни с точки зрения физика", результаты этой работы оказались интересными в основном для самих физиков и для широкой публики. Разрабатываемые вне связи с экспериментальными исследованиями, эти "модели старения" оказались абсолютно неадекватными с точки зрения биолога.

Но новом этапе цели математического моделирования связаны в первую очередь с желанием усовершенствовать процесс извлечения информации о механизмах старения и защитных механизмах у экспериментальных животных на основе реальных наблюдаемых в эксперименте данных. Математические модели позволяют выдвигать биологически обоснованные и формально корректные гипотезы о таких механизмах и тестировать их. Поэтому не удивительно, что в последнее время практически все ведущие экспериментальные команды в мире, ведущие исследования механизмов старения на популяциях насекомых, включили в свой состав специалистов по моделированию.