В условиях равновесия рассматриваемая схема взаимодействия

описывается системой следующих алгебраических уравнений:

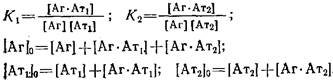
Опуская алгебраические преобразования, дадим окончательное выражение зависимости, описывающей связь параметров системы в координатах Скэтчарда:

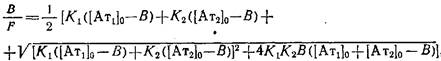
где В = Вй-\-В2=+; F=. Графическая зависимость B/F от В имеет вид гиперболы. Таким образом, получаемая при анализе зависимости связывания неизвестной популяции антител с антигеном в координатах Скэтчарда вогнутая кривая может свидетельствовать о существовании двух фракций антител — высокоаффинной и низкоаффинной.

Для определения четырех неизвестных параметров — Кй, Кг, 0 и о можно воспользоваться одним из следующих методов.

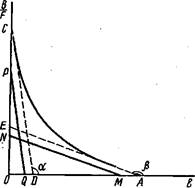
1. Параметры можно оценить по углам наклона асимптот гиперболы и отрезкам, отсекаемым ими на оси абсцисс и ординат. Для построения асимптот используют следующий прием. По концевым участкам экспериментальной кривой проводят прямые, которые дают первоначальное приближение констант Кй и Кя.Путем параллельного перемещения прямых подбирают такое их положение, чтобы сумма отрезков, отсекаемых ими на осях координат', была равна соответствующим отрезкам на тех же осях, отсекаемых самой кривой при экстраполяции ее к осям координат:

Отрезки на оси абсцисс ОМ и оси ординат CW дают оценочные значения для 0 и о соответственно. Подставляя оценочные значения Кй, Кз, 0 в выражения для Вй и В2

находят приближенные параметры В\ и В% и В=В1-\-В2 при различных концентрациях Аг.

С использованием полученных значений строят теоретическую зависимость B/F от В, сравнивают ее с экспериментальной и подбирают новые оценочные параметры до наилучшего совпадения теоретической и экспериментальной кривой.

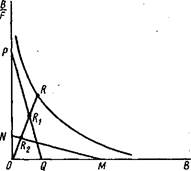
2. Для нахождения асимптот гиперболы можно воспользоваться чисто графическим методом, заключающимся в построении двух прямых PQ и НМ, для которых выполняется соотношение

т. е. отрезок OR, соединяющий начало координат с любой точкой R, находящейся на гиперболе, равен сумме отрезков ORi и OR2, соединяющих начало координат с точками пересечения отрезка OR с асимптотами.

3. Для оценки параметров Ки Кг, п и о часто используют следующий метод, основанный на анализе графической зависимости B/F от В. Из экспериментально полученной кривой связывания путем экстраполяции находят точки пересечения кривой с осями абсцисс и ординат. Проводят касательные в этих точках к кривой до пересечения их с осями абсцисс и ординат в точках D и Е„

Можно показать, что численные значения искомых параметров определяются по следующим алгебраическим формулам:

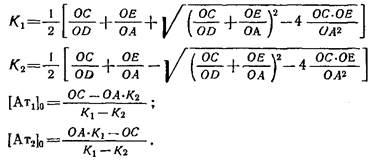
3. Кинетические закономерности реакции взаимодействия антиген — антитело

Образование комплекса антиген—антитело является обратимым процессом, т. е. равновесная константа связывания данного комплекса определяется отношением константы скорости ассоциации ki к константе скорости диссоциации. Исследование кинетики процесса комплексообразованияантигенов с центрами связывания антител в широком диапазоне концентраций, включая избыточные концентрации каждого из реагентов, позволяет определить значения кинетических констант скоростей ассоциации и диссоциации, рассчитать время, необходимое для достижения системой равновесия. -

Реакция антиген—антитело в диапазоне таких концентраций реагентов, которые регистрируются обычны» ми физнко-химическимн методами, протекает очень быстро, что затрудняет ее изучение с помощью традиционных кинетических.методов,

При высоких концентрациях реагентов лимитирующим фактором является время смешивания растворов, так как равновесие устанавливается за время, которое не позволяет определять изменения концентраций реагентов.

Для нахождения кинетических констант реакции антиген—антитело могут быть применены два экспериментальных подхода. Первый из них состоит в использовании специальных приемов для изучения быстрых реакций — метода температурного скачка и метода остановленной струи. Второе направление связано с применением реагентов, позволяющих следить за реакцией комплексообразования в области ультранизких концентраций реагентов. Переход к низким концентрациям реагентов дает возможность значительно понизить скорость реакции и использовать для расчетов традиционные кинетические методы.

Основная часть кинетических экспериментов, приведенных в литературе, выполнена, для взаимодействия гаптенов, главным образом ДНФ-лигандов. Лишь очень небольшое количество работ посвящено кинетическому исследованию взаимодействия антител с антигенами белковой природы. Это связано с тем, что кинетические данные, полученные в опытах со сложными антигенами, трудно интерпретировать.

Как для белковых антигенов, так и для гаптенов установлены достаточно высокие значения констант скоростей ассоциации, приближающиеся к диффузионно контролируемому пределу. В случае белковых антигенов их значения приблизительно на 2 порядка меньше и колеблются от 5-105 до 5-Ю6 М-1-с-1, что объясняется более сложной структурой антигенной детерминанты белковых антигенов.

Имеющиеся данные свидетельствуют о том, что наблюдаемые различия в аффинности антител обусловлены, в основном, значениями константы скорости диссоциации. Это было наглядно продемонстрировано в экспериментах с серией гомологичных гидрофобных ДНФ-лигандов, в которых десятикратное увеличение константы аффинности для двух перекрестно реагирующих ли-гандов обусловлено различием в константах скоростей диссоциации, а не ассоциации. Эти и другие результаты показывают, что именно константа скорости диссоциации определяет сродство антитела к гаптену. Этот вывод, однако, нельзя считать окончательным, поскольку количество экспериментальных данных, полученных к настоящему времени, ограничено.

Экспериментальные методы определения кинетических констант. Метод температурного скачка. Этот метод является одним из релаксационных методов, основанных на принципе зависимости времени достижения нового равновесного состояния системы, обусловленного быстрым внешним воздействием, от констант скоростей прямой и обратной реакций. Можно показать, что если в начальном состоянии система

находится в равновесии, то после быстрого изменения температуры кинетика реакции достижения нового положения равновесия описывается дифференциальным уравнением, решение которого представляет собой экспоненту, в которой показатель экспоненты связан с элементарными константами скоростей реакции уравнением