Решение

Применим формулу сложных процентов и рассчитаем наращенную сумму первоначального взноса через 3 года под 14% годовых:

S1 =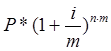

где

Р – сумма первоначального взноса;

i – годовая процентная ставка;

n – период начисления процентов;

m – количество начислений процентов в год.

Тогда:

S1 = = 3795,66 руб.

Теперь рассчитаем наращенную сумму взносов

Последовательный регулярный ряд выплат называют финансовой рентой или аннуитетом. При этом если выплаты осуществляются в конце периода, то имеет место финансовая рента постнумерандо, если в начале периода – финансовая рента пренумерандо. Если выплаты осуществляются один раз в год – это годовая рента, если р- раз в год – р-срочная рента.

Будущая стоимость финансовой р-срочной ренты постнумерандо определяется по следующей формуле:

(1 + i/m)nm – 1

S(n) = X ——————

(1 + i/m) m/p –1

где i – годовая номинальная ставка сложных процентов;

Х – член ренты;

n – период ренты (лет);

m – число раз начисления процентов в год;

p – число осуществления выплат в год.

По условию задачи: i = 0,14 (14%); n = 3 года; m = 12; p = 12; Х = 300 руб.

Тогда сумма, которая будет накоплена к выходу на пенсию составит:

(1 + 0,14/12) 3*12 – 1

S2 = 300* ———————— = 13326,84 (рублей)

(1 + 0,14/12)12 / 12 – 1

Окончательно рассчитываем сумму, накопившуюся на счете в конце срока:

S = S1 + S2 = 3795,66 + 13326,84 = 17122,5 (рублей)

Вопрос 3

Рыночная стоимость объекта недвижимости составляет 2500000 долларов. Согласно договору купли-продажи первоначально выплачивается 50% стоимости, а оставшаяся сумма погашается в течение 2 лет ежемесячными платежами. Рассчитать величину платежей, если ставка дисконтирования (начисление процентов производится 12 раз в год) выбрана 10%.

Решение

Рассчитаем текущую стоимость единичного платежа по следующей формуле:

,

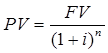где PV – текущая стоимость платежа;

FV – будущая стоимость платежа (номинальная сумма денежной выплаты);

i – ставка дисконтирования;

n – количество периодов, через которое ожидается поступление (выплата) денежных средств.

Если производится серия платежей, то в общем случае для каждого из них придется применять данную формулу. Однако расчет можно упростить, если речь идет о серии равновеликих платежей через одинаковые промежутки времени. Такие последовательности называются аннуитетами. Тогда формула расчета текущей стоимости примет следующий вид:

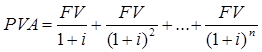
где PVA – текущая стоимость платежа;

FV – будущая стоимость единичного платежа для данного аннуитета;

i – ставка дисконтирования;

n – количество периодов, за которые производятся выплаты или ожидаются поступления денежных средств.

Если вынести общий множитель FV за скобки и свернуть сумму факторов дисконтирования по формуле суммы членов геометрической прогрессии, получим следующее выражение:

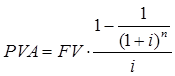
Данная формула действительна, если платежи производятся раз в год.

Для случая платежей m раз в году имеем:

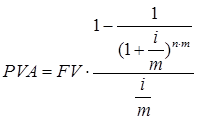
По условию задачи:

PVA = 2500000*50% / 100% = 1250000 (долларов)

n = 2 (года)

m = 12

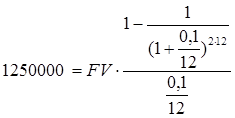
Тогда, величина ежемесячных платежей:

(долларов) – искомая величина ежемесячных платежей.