Модель реальных опционов предоставляет менеджерам возможность планирования и управления стратегическими инвестициями и представляет синтез оценки рыночной стоимости и принятия инвестиционных решений в условиях неопределенности. Так, модель реальных опционов объединяет методику проектного анализа и формирования корпоративной стратегии.

Для оценки как реальных, так и обычных опционов применяются в основном две модели:

· Биноминальная модель;

· Модель Блека-Шоулза.

Эти модели играют большую роль в инвестиционном анализе. Рассмотрим и дадим оценку каждой из них.

2.2 Биноминальная модель оценки опциона

Для оценки стоимости опциона «колл» или «пут» можно использовать биноминальную модель оценки стоимости опциона (ВОРМ). Лучше всего представить ее на примере европейского опциона (European option), т.е. опциона, который может быть исполнен только в день его истечения. В этом случае мы предполагаем, что по базисной акции не выплачиваются дивиденды в течение срока действия опциона. Модель также можно модифицировать для оценки стоимости американского опциона (American option), т.е. опциона, который можно исполнить в любое время в течение срока действия опциона. Модель также можно использовать для оценки стоимости опционов на акции, по которым выплачиваются дивиденды в течение срока опционного контракта.

Биномиальный метод, называемый также по имени его авторов методом Кокса-Росса-Рубинштейна (Cox-Ross-Rubinstein), был предложен в 1979 году и является более поздним по отношению к методу Блэка- Шоулса (1973). Однако начинать знакомство с подходами к оценке опционов лучше именно с более простого биномиального метода. В определенном смысле он аналогичен численным методам решения дифференциальных уравнений. Первоначально данный подход применялся для расчета стоимостей американских опционов, для которых отсутствует точное аналитическое решение, а впоследствии был распространен на многие более сложные производные инструменты. В настоящее время численные методы наряду с методами статистических испытаний (Монте-Карло) чаще всего используются в моделях обсчета производных инструментов, так как позволяют максимально учесть реальные условия операций с ними.

В биноминальной модели весь период действия опционного контракта разбивается на ряд интервалов времени; в рассматриваемом ниже случае – на два периода. Предполагается, что стоимость опциона и стоимость базового актива (в данном случае акции) изменяется согласно разветвленной системе на рис.14. Учитывая данные о стандартном отклонении курса базисного актива, получают значения его цены для каждого интервала времени (строят дерево распределения цены). Так же определяют вероятность повышения и понижения курсовой стоимости актива на каждом отрезке временного интервала. Имея значения цен актива к моменту истечения срока действия опциона, определяют его возможные цены в данное время. После этого последовательным дисконтированием цен опциона (с учетом вероятности повышения и понижения стоимости актива на каждом интервале времени) получают значение его цены в момент заключения контракта.

uS0 Сu1

S0 С0

dS0 Сd1

Рисунок 14 Биноминальная модель ценообразования опционов

Техника построения биномиальной модели является более громоздкой, чем метод Блэка—Шоулза, но позволяет получить более точные результаты, когда существует несколько источников неопределенности или большое количество дат принятия решения.

В основе модели лежат два допущения:

·в одном интервале времени могут быть только два варианта развития событий (худший и лучший);

·инвесторы нейтрально относятся к риску.

Простейший пример использования биномиальной модели для расчета стоимости инвестиционного проекта уже был использован выше. Напомним, что мы рассматривали проект с одним интервалом времени и двумя вариантами реализации решений. Для каждого варианта была оценена вероятность наступления и рассчитана стоимость реального опциона. Вычисление стоимости опциона данным методом, по сути, представляет собой движение по «дереву решений», где в каждой точке менеджеры стараются принять наилучшие решения. В итоге денежные потоки, возникающие как следствие будущих решений, сводятся к приведенной стоимости. Однако в реальной жизни «дерево решений», как правило, имеет гораздо больше узлов принятия решений (рис.15)

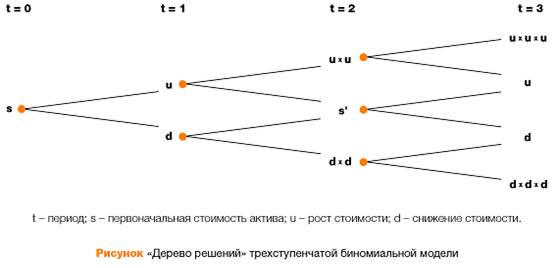
При построении «дерева решений» с большим количеством дат принятия решений применяются те же принципы расчета стоимости реального опциона, что и для рассмотренной выше одноступенчатой модели. Однако чем больше узлов принятия решений, тем сложнее сделать оценку.

На практике основные трудности использования биномиальной модели связаны с определением значений относительного роста и снижения стоимости бизнеса в каждом периоде, а также вероятностей положительного и негативного варианта развития событий. Для расчета этих параметров разработаны соответствующие формулы. Возможный рост стоимости бизнеса рассчитывается как:

u = es,

где u — относительный рост (значение данного параметра, например 1,25, означает ожидаемый рост стоимости проекта в 25%);

s — стандартное отклонение среднегодовой стоимости проекта;

h — интервал как часть года (к примеру,

h = 0,5, если решение по проекту принимается раз в полгода).

Относительное снижение стоимости (d) рассчитывается по формуле

d = 1 : u.

Тогда вероятность относительного роста (П), исходя из предположений о нейтральном отношении к риску, можно рассчитать как:

П = [(1 + r) — d ] : u - d.

Соответственно вероятность снижения стоимости проекта будет равна

1- П.

Таким образом, исследовав биноминальную модель можно сказать о том, что эта модель имеет важное значение при анализе инвестиционного проекта. С помощью нее можно рассчитать стоимость опциона, зная цену актива и предположить как будет расти цена инструмента в зависимости от цены его актива.

Если бы мы исследовали случай с несколькими периодами, портфель (акции, облигации и опционы) нужно было бы скорректировать: в нем должно быть столько ценных бумаг каждого вида, чтобы портфель всегда был хеджированным. Если периоды времени сокращаются и операции совершаются непрерывно, то мы приходим к модели оценки опционов Блэка— Шоулса. Модель Блэка—Шоулса не противоречит биномиальной модели, описанной в этом разделе, если предположить, что операции совершаются непрерывно и в очень короткие периоды. Оценка стоимости опционов с помощью биномиального метода при достаточно большом количестве дат принятия решений на протяжении года будет близка к значению, полученному с использованием модели Блэка—Шоулза.