Ai- постоянный параметр (не зависит от времени), показателей, какая часть доходности i-й ценной бумаги не связана с изменениями доходности рыночного портфеля ценной бумаги rт (t);

Bi- постоянный параметр, называемый бета, показывающий чувствительность доходности 1-й ценной бумаги к изменениям доходности рыночного портфеля;

rт (t)- доходность рыночного портфеля, включающего в идеале все ценные бумаги рынка (хорошая аппроксимация — фондовый индекс типа S&Р500) в момент времени t;

Ei(t)- случайная ошибка.

Основное допущение этой модели заключается в предположении, что доходность отдельной ценной бумаги зависит в основном от доходности рынка в целом. И это допущение позволяет значительно снизить объем вычислений, что и является главным достоинством модели Шарпа. Не нужно рассчитывать корреляцию с каждым отдельным активом портфеля, а только с рыночным портфелем.

Параметр Bi (бета) определяет зависимость доходности i-й ценной бумаги Ri(t) от рыночной доходности rт (t).

При Bi > 0 — динамика доходности ценной бумаги аналогична динамике доходности рыночного портфеля. Доходность ценной бумаги возрастает при росте доходности рынка.

При Bi > 1 — этот эффект сильнее, а ценная бумага рискованнее, поскольку при падении биржевого индекса потеряет свою доходность и ценная бумага.

При Bi < 0 — эффект ценной бумаги обратен эффекту рынка. Доходность ценной бумаги возрастает при снижении доходности портфеля рынка. И наоборот.

При использовании формулы для Ri(t) ожидаемая доходность портфеля из М ценных бумаг будет равна:

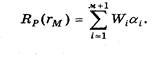
Ожидаемая доходность портфеля R(rт) есть сумма двух членов (см. подробный вывод, например):

сумма взвешенных параметров i каждой ценной бумаги — вклад в ожидаемую доходность самих ценных бумаг;

Члена

произведения портфельной беты на ожидаемую доходность рыночного портфеля, что отражает влияние на доходность портфеля из М ценных бумаг рынка. Величина

представляет собой сумму взвешенных величин «беты» Bi каждой ценной бумаги (где весом служат Wi) и называется портфельной бетой Bт. Портфельная бета отражает влияние рынка на весь инвестиционный портфель в целом.

Отметим основные этапы, которые необходимо выполнить для построения границы эффективных портфелей в модели Шарпа.

1. Выбрать М ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N шагов расчета, за который будут наблюдаться значения доходности гit для каждой ценной бумаги.

2. По выбранному рыночному индексу вычислить рыночные доходности rтt для того же промежутка времени.

3. Определить величину дисперсии рыночного показателя ат2, а также значения ковариаций аiт доходностей каждой ценной бумаги с доходностью рыночного портфеля (его аппроксимацией — подходящим фондовым индексом) и найти величины Д:

4. Найти ожидаемые доходности каждой ценной бумаги Ri(ri) и доходности рыночного портфеля Rр(rт) и вычислить параметр:

5. Вычислить дисперсии случайных ошибок е

6. Подставить эти значения в соответствующие уравнения.

После такой подстановки выяснится, что неизвестными величинами являются веса Wi ценных бумаг. Выбрав определенную величину ожидаемой доходности инвестиционного портфеля, можно найти веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель.

Список литературы

1.Корчагин Ю.А., Маличенко И.П.Инвестиции. –Р-н/Д: Феникс, 2008

2.Нешитой А.С.Инвестиции. –М.: Дашков и Ко, 2007

3.Ример М.И., Касатов А.Д., Матиенко Н.Н. Экономическая оценка инвестиций. –СпБ: Питер, 2007

4.Янковский К.П. Инвестиции.- СпБ: Питер, 2008

Приложение А

Схема: Содержание и основные этапы формирования инвестиционной политики предприятия (корпорации) рисков, связанных с выполнением конкретных проектов

Приложение Б

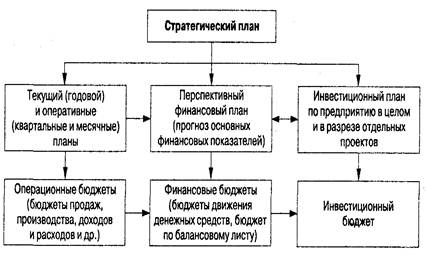
Схема: Взаимосвязь между системой планов на предприятии, реализующем инвестиционные проекты