Например, предприятие получает в банке 10 млн. рублей на 1,5 года под номинальную ставку 22% годовых с ежемесячным реинвестированием начисленных процентов. По условиям кредитного договора уплата банку начисленных процентов должна производиться ежеквартально в течение всего срока ссуды. По окончании срока предприятие должно вернуть банку основную сумму долга. Таким образом, каждые три месяца предприятие должно будет выплачивать банку по 560,15 тыс. рублей (расчеты выполнены по формуле (2.2.13) с параметрами: P = 10000 тыс. руб., n = 0,25 года (1 квартал = 1/4 или 3/12 года), m = 12, j = 22%). Последняя выплата в конце срока составит 10560,15 тыс. рублей (10000 + 560,15). Полуторагодовой период включает в себя 6 кварталов, следовательно денежный поток по данной операции будет иметь вид: (+10000; -560,15; -560,15; -560,15; -560,15; -560,15; -10560,15). YTM этого потока найдем из формулы (5.2.2):

Она составит 24,36%. Так как проценты по банковскому кредиту включаются в состав себестоимости продукции, скорректируем полученный результат на эффект налогового щита:

Kd = 0,2436 * (1 – 0,3) = 17,052%

Цена заемного капитала составит в этом случае 17,052%.

Предположим теперь, что банк согласен на получение всей суммы начисленных процентов в конце срока ссуды, то есть он не настаивает на ежеквартальной выплате процентов. Сначала рассчитаем по формуле (2.2.13) наращенную сумму кредита к концу его срока:

Тогда денежный поток будет иметь вид (+10000; -13868,17). По формуле находим, что его уравнивает эффективная процентная ставка 24,36%, то есть для предприятия этот вариант абсолютно равнозначен предыдущему и периодичность выплаты начисленных процентов не оказывает влияния на цену привлекаемого капитала. Точно такой же результат будет получен, если рассчитать сложную эффективную процентную ставку, эквивалентную номинальной ставке 22% годовых. По формуле получаем:

Следовательно, оба варианта погашения процентов по кредиту обусловливают одну и ту же цену заемного капитала: 24,36% или 17,052% с учетом налогообложения.

Задача 7

Американская компания “Red Tape” в 2005 г. имела большой успех на рынке Восточной Европы и, стремясь как можно быстрее расширить свое влияние в этом регионе до прихода конкурентов, приняла решение об увеличении производственных мощностей в два раза. Для этого ей требовалось дополнительно 1 млн. дол. По поводу источников финансирования разгорелись жаркие споры.

Рассматривались два варианта:

1. Эмиссия обыкновенных акций на сумму 1 млн. дол. в количестве 10 тыс. штук номиналом 100 дол.;

2. Эмиссия облигаций на сумму 1 млн. дол. в количестве 10 тыс. штук номиналом 100 дол.

Первый вариант предложил президент компании Джонсон, а второй вариант отстаивал председатель Совета директоров Бриг.

Бриг имеет контрольный пакет акций компании, акционерный капитал которой к моменту спора равнялся 1 млн. дол. Доля Брига составляла 52%. Если будет принят первый вариант, то его доля уменьшится вдвое. При эмиссии облигаций, величина акционерного капитала останется прежней и это устраивало Брига.

По мнению Джонсона эмиссия облигаций, увеличивая уровень задолженности компании в целом, ухудшает показатель финансовой устойчивости. Даже предложение Брига понизить ставку дивиденда до уровня ставки по облигациям (10% годовых) не повлияло на мнение Джонсона, считающего, что это не дает никакого выигрыша для компании.

Какой вариант поддержали бы Вы?

Обоснуйте расчетами, используя дополнительную информацию:

а) ставка налога на прибыль - 24%;

б) экономическая рентабельность чистых активов - 25%.

Решение:

Чаще всего при оценке доходности акций исходят из предположения устойчивого роста дивидендов: сумма доходов, выплачиваемых инвестору по акции, увеличивается с неизменной скоростью (темпом прироста) g. Для изучения подобных процессов используется модель Гордона (см. параграф 3.4). В этом случае доходность акции рассчитывается по формуле (5.3.5). Принимая во внимание расходы по размещению акций на рынке (CEm), получаем цену акционерного капитала (Kes):

,

где Div1 – дивиденды на одну акцию, ожидаемые в первом планируемом году;

P – рыночная цена 1 акции;

CEm – абсолютная сумма расходов по эмиссии в расчете на 1 акцию;

l – относительная величина расходов на эмиссию в процентах (l = CEm / P);

g – ожидаемый темп прироста дивидендов в последующие годы.

Например, по акции, рыночная стоимость которой 200 рублей, ожидается выплата годового дивиденда в сумме 50 рублей, который ежегодно будет увеличиваться на 2%. Расходы по эмиссии составляют 5% от фактической цены. Используя формулу, находим, что цена капитала данного вида составит:

Предположение о неизменном темпе прироста дивидендов не является незыблемой догмой, предприятие-эмитент может планировать постоянную из года в год сумму дивидендных выплат, а может, напротив, заложить в свои прогнозы более сложную модель роста – равноускоренное или переменное увеличение. В первом случае формула расчета доходности упростится и цену капитала можно будет найти как процентную ставку перпетуитета:

,

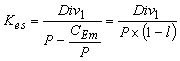где Div1 – размер ожидаемых дивидендов на 1 акцию;

P – рыночная цена 1 акции;

CEm – расходы на эмиссию;

l – доля расходов по эмиссии в цене одной акции (СEm / P).

В нашем примере это будет означать отсутствие в выражении (6.3.2) темпа прироста дивидендов g, в результате чего цена капитала снизится на 2 процентных пункта и составит 26,316% (28,316% - 2%).

Второй случай предполагает использование более сложных математических моделей. Однако, усложнение расчетов оправдано только тогда, когда имеется уверенность в способности компании обеспечить заданные темпы прироста дивидендов. Учитывая высокую рискованность акционерного капитала, можно утверждать, что далеко не каждое предприятие способно обеспечить соблюдение данного условия на достаточно длительном промежутке времени. Тем более, когда речь идет о российских предприятиях, еще не накопивших существенного опыта работы в условиях свободного рынка. Поэтому, при определении цены акционерного капитала обычно не ограничиваются каким-то одним (пусть даже самым сложным) способом расчета, а одновременно применяют несколько более простых методов. Причем, ни один из них не рассматривается как идеальный. Используя различные подходы, финансист стремится минимизировать разброс получаемых результатов, пытаясь найти некое консенсусное значение, которое может быть обосновано не только математическими расчетами и логическими построениями, но и его (финансиста) интуицией и здравым смыслом.