Полиномы Чебышева

Критерии согласия данного метода — минимизация максимальной ошибки.

Полиномы Чебышева определяются следующим образом: Tn(x)=cos(n×arccos(x))

Например: T0(x)=cos(0)=1,

T1(x)=cos(q)=x,

T2(x)=cos(2q)=cos2(q)-sin2(q)=2x2-1.

Можно было бы и дальше использовать тригонометрические соотношения для нахождения полиномов Чебышева любого порядка, но будет лучше установить для них рекурентное соотношение, связывающее Tn+1(x), Tn(x) и Tn-1(x):

Tn+1(x)=cos(nq+q)=cos(nq)cos(q)-sin(nq)sin(q),

Tn-1(x)=cos(nq-q)=cos(nq)cos(q)-sin(nq)sin(q).

Складывая эти неравенства, получим:

Tn+1(x)+Tn-1(x)=2cos(nq)cos(q)=2xTn(x);

Tn+1(x)=2xTn(x)-Tn-1(x).

Применяя полученные формулы можно найти любой полином Чебышева. Например, Т3(x)=2xT2(x)-T1(x). Подставляя значения T2(х) и Т1(х) имеем Т3(х)=2х(2х2-1)-х=4х3-3х. Графически первые 10 полиномов Чебышева изображены ниже. Последующие полиномы по-прежнему колеблются между +1 и -1, причём период колебания уменьшаются с ростом порядка полинома.

Преобразования q=arccos(x) можно рассматривать как проекцию пересечения полукруга с множеством прямых, имеющих равные углы между собой (рис.1). Таким образом, множество точек xj, на котором система чебышевских многочленов Tn(x) ортогональна, таково:

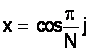, (j=0, 1, 2, …,N-1)

Так как Tn(x) есть, по существу, cos(nq), то они являются равноколеблющимеся функциями, и так как они многочлены, то обладают всеми свойствами ортогональных многочленов.

Чебышев показал, что из всех многочленов Рn(x) степени n старшим коэффициентом 1, у многочлена точная верхняя грань абсолютных значений на интервале -1£x£1 наименьшая. Так как верхняя грань Tn(x)=1, указанная верхняя грань равна .

Практическое задание

На практике нам нужно было изучить приближение нашей функции полиномами Тейлора.

Как уже упоминалось выше, многочлены Тейлора легко вычислять, а так же превращать в степенные ряды. В этом мы и убедились на практике.

Ниже представлена таблица коэффициенты первых 12-и полиномов Чебышева, а также таблица коэффициентов перед полиномами Чебышева, выражающие первые 12 степеней х.

Эти данные мы получили, используя программы на страницах

В этих программах использовались следующие алгоритмы:

I. Преобразование коэффициентов полинома Чебышева в коэффициенты традиционного многочлена.

1) Вводим коэффициенты a0, a1, …, an многочлена T(x) и образуем массив ai.

2) Для j=2, 3, …, n и k=n, n-1, …, j в первом случае поднимаясь, а во втором спускаясь, проводим преобразование коэффициентов по следующим формулам:

а) ak-1=ak-2-ak

б) ak=2ak

В результате получаем коэффициенты полинома Pn(x)

II. Преобразование коэффициентов полинома Pn(x) в коэффициенты полинома Tn(x)

1) Вводим коэффициенты полинома Pn(x) — аi

2) Для j=n, n-1, …, 2 и k=j, j+1, …, n в первом случае спускаясь, а во втором поднимаясь, проводим преобразование коэффициентов по следующим формулам:

а) ak=ak/2

б) ak-2=ak-2+ak

с) a0=2a0

В результате получим коэффициенты полинома Тn(x). Любопытно было бы узнать, какую ошибку мы получаем при разложении степенной функции по полиномам Чебышева. Для этого, используя выше описанные алгоритмы, я сначала представлял функцию y=xn (где n брал от 1 до 10) через полиномы Чебышева (Tn), а затем чтобы оценить ошибку чебышевское разложение снова превращал в многочлен. Выполнив эти операции, я получил достаточно интересные результаты. Для нечётных n ошибка настолько мала, что её едва можно различить на графиках (стр. ). Для чётных же степеней мы наблюдаем смещение графика, полученного в результате преобразования, вниз относительно оригинала. Это можно объяснить следующим образом. За смещение графика несёт ответственность коэффициент перед x0. Вспомним алгоритмы, они построены так, что каждый предыдущий коэффициент вычисляется через последующий. То есть в результате накапливающаяся ошибка вычисления больше всего влияет на коэффициент при x0. Следствием этого является смещение графиков чётных степеней, так как в их разложении присутствует этот коэффициент. Заметим также, что смещение при разложении функции y=x2 больше, чем при разложении функции y=x10. Этот тоже легко объяснить, так как при увеличении степени вклад T0 в разложении степенной функции уменьшается. Что же касается нечётных степеней, то мы получили такое хорошее совпадение так как чётные коэффициенты в разложении нечётных степеней равны 0, а коэффициенты при всех степенях x, кроме нулевой влияют лишь на отклонение ветвей. Подтверждением этого служат графики на странице .

Следующим этапом работы являлось приближение полиномами Чебышева произвольной функции. В качестве исходной функции я взял функцию y=sin(4x/3). Используемая в работе программа представлена на странице . Для её написания был использован следующий алгоритм:

I. Приближение функции f(x) по Чебышеву.

1) Задаём степень n многочлена Tn(x) и пределы [a; b] изменения аргумента функции f(x).

2) Для i=0, 1, …, n на отрезке [-1; 1] формируем сетку оптимальных значений аргумента в узлах чебышевской интерполяции:

.

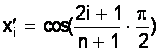Переводим в отрезок [a; b]:

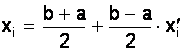и вычисляем f(xi)

3) Для k=0, 1, …, n и i=0, 1, …, n вычисляем:

.

В результате получаем коэффициенты a0, a1, …, an многочлена T(), приближающего функцию f(x).

II. Вычисление значений T(x) выполняется по следующему алгоритму:

1) Считая заданным массив ak, задаём память под массив из n+2 вспомогательных коэффициентов bk. Полагаем bn+2=0, bn+1=0.

2) Задаём значения x на [a; b] и переводим их в отрезок [-1; 1] с помощью преобразований:

.

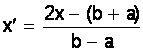3) Для k=n, n-1, …, 1 вычисляем bk=ak-bk+2+2xbk+1.

4) Находим T()=a0/2 - b2 +xb1

Также в программе было использовано разложение в ряд Тейлора для сравнения с разложением по полиномам Чебышева. Прежде всего я рассмотрел приближение на интервале [-1; 1]. Наложив на график sin(4x/3) график его приближения полиномами Чебышева и график, построенный с помощью разложения в ряд Тейлора, я получил очень точное совпадение. Визуально нельзя различить три кривых. Рассмотрим график ошибок. В соответствии с теорией ошибка Чебышева знакопеременна и распределена более или менее равномерно по всему интервалу. Ошибка же Тейлора небольшая около 0 и сильно увеличивается при приближении к 1 (заметим, что в этом и в других случаях ряд Тейлора содержит те же степени x, но с другими коэффициентами). Интереснее рассмотреть приближение на более длинных интервалах. На интервале [-1; 1] приближение полиномами Чебышева 7-й степени достаточно хорошее, но уже на интервале [-10; 10] приближение этой же степенью очень плохое (стр. ). Рассмотрим приближение на этом же интервале полиномом более высокой степени (T11). Получим неплохое приближение, причём на графике очень чётко видно, что ошибка распределена равномерно. Здесь опять хотелось бы сравнить с разложением в ряд Тейлора. Если посмотреть на графики на странице , мы увидим, что приближение с помощью рядов Тейлора очень хорошее в середине интервала, но сильно отклоняется от эталона на концах. Сравним ошибки чебышевского приближения и приближения с помощью рядов Тейлора. При этом сравнении ясно проявляются свойства полиномов Чебышева — максимальная ошибка меньше, чем при использовании ряда Тейлора.