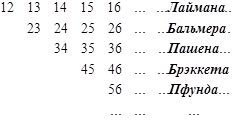3.1. Энергия поглощаемого или испускаемого фотона - кванта электромагнитного поля прямо пропорциональна частоте излучения , обратно пропорциональна длине волны , прямо пропорциональна волновому числу  и определяется известной формулой Планка:

(3.1)

Это соотношение позволяет для отсчёта энергии использовать и единицы измерения частоты (1 герц = с-1 или кратные ему величины 1 килогерц =103 герц, или1ме-гагерц =106 герц, или 1 гигагагерц =109 герц и т.д.), и единицы измерения волнового числа (чаще всего обратные сантиметры []  см-1). Эти разные шкалы отсчёта энергии используются в различных областях экспериментальной спектроскопии.

Так, например, в оптической спектроскопии, изучающей электронные переходы в атомах и молекулах, используются обратные сантиметры (см-1), в радиоспектроскопии, изучающей процессы переориентации векторов магнитных моментов электронов или ядер (спиновых векторов ядер или электронов), обычно применяет единицы частоты - мегагерцы или гигагерцы (мГц, гГц,). В спектроскопии высоких энергий, использующей рентгеновское или гамма-излучение, обычной единицей является электроновольт (эВ).

3.2. Уровни квантовых систем являются элементами одномерных массивов - энергетических спектров и могут быть пронумерованы каким-либо дискретным числовым множеством, чаще всего , где квантор V означает «или»

. (3.2)

Числа-номера уровней называются квантовыми числами. Они образуют массивы. Дис-танции между уровнями образуют уже двумерные упорядоченные массивы - матрицы:

. (3.3)

Каждой паре уровней соответствует два перехода. Энергии поглощаемого и испускаемого квантов (поглощаемого или испускаемого фотона) почти одинаковы, и эту пару переходов удобно изобразить символом или можно просто парой индексов, которые в зависимости от направления перехода чередуются как nm (переход n ® m) или как mn (переход m ® n).

3.3. Поглощение или испускание фотона системой по закону сохранения энергии связано с её переходами вдоль лесенки дискретных уровней энергии, и поэтому каждому из возможных переходов отвечает своя частота или своё волновое число. Частоты, волновые числа и длины волн, порождаемые этими квантовыми переходами, характеризуют электромагнитный спектр системы. Они также образуют матрицы и могут быть пронумерованы индексами:

.(3.4)

Упорядоченная сводка характеристик системы, которые зависят от пар уровней, всегда представляет собой двумерную матрицу. Её структура проста и совпадает с принципом нумерации её элементов :

По такой схеме получается спектр частот электронных переходов в атомарном водороде.

3.4 Атом водорода, уровни и переходы, частоты и спектральные серии

(Упражнения для практического занятия.)

3.4.1. Уровни энергии.

Выше была выведена формула Бора для уровней энергии водородоподобного иона. Это электронные уровни. Состояния одной частицы принято называть орбиталями, поэтому эти уровни называют также орбитальными:

(3.5)

Z -порядковый номер элемента. –приведённая масса (»e) .

Орбитальные уровни дискретны, и это выражается в том, что в формулу входит переменная, у которой просто не бывает нецелочисленных значений. Это квантовое число n.

3.4.2. Универсальные мировые постоянные равны:

3.4.3. Формула Бора может быть записана в очень простом виде. (Z=1).

Для этого универсальные константы объединяются в один множитель, получая:

Спектр энергетических уровней приобретает вид:

Упорядочим размерности, а именно:

,

поскольку

Используя приведённую массу, находим A=2.1787221 эрг×см.

3.4.4. Спектральные переходы характеризуются волновыми числами (или частотами):

.(3.6)

Наиболее просто это выглядит как

(3.7)

3.4.5. Постоянная Ридберга это коэффициент R. Её значение:

В спектре атомарного водорода (рис.) возникают следующие серии

Формуле (3.7) можно придать очень простой матричный вид

, где , (3.8)

3.4.6. Диагональные матричные элементы нулевые и не имеют смысла. Переходам отвечают лишь недиагональные матричные элементы ; все они содержатся в одной из двух треугольных субматриц, лежащих одна - над-, а вторая - под нулевой диагональю, и .

Элементы положительной матрицы представляют собой рациональные дроби, равные:

n 1 2 3 4 5 . серия m

Умножением этих матричных элементов на константу Ридберга, получается матрица волновых чисел переходов в единицах волнового числа (см-1):

3.4.7. Спектральные серии представляют собою строки в этой матрице.