1. Активность

Рассмотренные нами соотношения для идеальных растворов не могут быть непосредственно использованы для вычисления равновесия, в котором участвуют реальные растворы, в частности в реальных растворах не выполняется один из основных законов химии – з. действия масс. При подставлении в выражения для константы равновесия концентрации реагирующих веществ константа равновесия оказывается не постоянно зависящей от концентрации. В случае идеальных растворов из измерения одного из свойств (давление пара) можно рассчитать все другие свойства. Желательно сохранить такую возможность для реальных растворов. Решение было предложено Льюисом, который ввел в теорию растворов так называемые т/д активности в качаестве ф-ии, связывающей свойства равствора друг с другом и заменил концентрацию в реальных растворах. Подставляя т/д активность в место концентрации, в т/д уравнение, полученное для идеальных растворов делает последнее пригодным и для реальных растворов. Т.о. активностью называется величина, подставляя которую вместо концентрации в т/д уравнение делает последнее применимым для реальных растворов, а – активность. После введения активного хим. потенциала i определяется соотношением Bb+dD↔Mm+rR. Константу равновесия определяет соотношение . З. распределения, если раствор 3-го вещества нельзя считать идеальным . Активность должна быть введена таким образом чтобы в идеальных растворах она совпадала с концентрацией, а в реальных растворах она должна характеризовать отклонение их от идеальных. По Льюису активность выражается соотношением давление пара данного компонента над реальным раствором к давлению пара этого компонента в некотором стандартном состоянии . Для растворимости в водных растворах для всех компонентов летучих жидких смесей. В начале стандартного состояния берут состояние компонентов в чистом виде и тогда при данной температуре . В совершенном растворе соотношение => в идеальном растворе активность = концентрации , в реальном растворе . Степень отклонения активности и концентрации определяется величиной коэффициента активности . В идеальном растворе , в реальном растворе может быть > и < 1. В разбавленных растворах для растворителя выполняется закона Рауля, а для растворов вещества з. Генри . Для растворённого вещества стандартное состояние должно быть сделано таким образом, чтобы в растворе любой концентрации соблюдался закон Генри , .

Связи м/у активностями компонентов

Уравнение Дюгема-Маргулиса:

(1). Если раствор является близким к совершенному, то , а . , . Продифиринцируем ( и =const) (2), (3). Подставим (4). Уравнение (4) может быть обобщено на раствор, содержащий несколько компонентов: 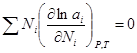. Если раствор близок к разбавленному для растворённого вещ-ва . Повторяя действие, что и здесь справедливо уравнение (4). Для бинарного раствора уравнение (4) имеет вид: , , 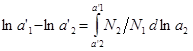. Если известна зависимость активности второго компонента от концентрации, а так же активность первого компонента для какой либо концентрации, то можно активность компонента для другой концентрации. Зная , можно подсчитать .

Методы определения активности

1) Определение активности по давлению пара, если компонент летучий; например, раствор олово-цинк близок к совершенному. Давление пара при 957К , а давление пара над сплавом олово-цинк, в котором молярная доля цинка 0,226, составляет . По определению, , а для летучего компонента . Коэффициент активности

2) Определение активности на основе закона распределения. В реальных растворах коэффициент распределения рассчитывается по формуле: , где и - активности распределяющегося вещества 1-ой и 2-ой фазы. При бесконечном разбавлении, когда количество введенного 3-го компонента невелико, активности равны соответствующим концентрациям, определяя которые, вычисляют к. . Если константа распределения велика, то при увеличении общего количества введенного 3-го компонента 2-й раствор может оставаться идеальным вплоть до насыщения и тогда закон распределения может быть представлен в виде: . Определяя С2 и зная константу, рассчитывают а1 , а1=КС2 – активность 3-го компонента в 1-ом растворе.