3. Решаем систему двух уравнений с двумя неизвестными x2 и r2:

Применяя так называемый метод последовательных приближений, выбираем произвольно некоторое начальное значение x2 = (x2)0, после чего находим (r2)0 и из следующего уравнения вычисляем значение x2 = (x2)1. Если бы начальное значение x2 было выбрано правильно, т.е. удовлетворяло бы уравнениям, то тогда (x2)0 = (x2)1. В противном случае (x2)0 ≠ (x2)1. Тогда с новым значением (x2)1 вычисляем аналогичным путем следующее приближение (x2)2. Если (x2)1 ≠ (x2)2, то вычисляем дальше и так до тех пор, пока два последующих приближения не сойдутся в пределах заданной точности.

4. Далее находим:

Координаты (xj ,yj, zj), j = 1,2,3 – прямоугольные гелиоцентрические экваториальные координаты тела в моменты 1, 2, 3 соответственно. Дальнейшее вычисление элементов орбиты может быть проведено по двум гелиоцентрическим положениям. Обычно выбирают два крайних положения, но я взял два положения, соответствующие моим снимкам 19.02 и 24.02.2009.

5. Вычисляем:

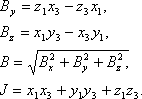
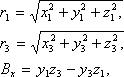
где x, y, z1 – эклиптические координаты кометы 19.02, а x, y, z3 – координаты на 24.02.

6. Находим элементы Ω (долготу узла), i (наклонение) по формулам:

После проведения этих вычислений, у меня получились такие результаты:

Ω ≈ 338,8º

i ≈ 178, 4º, что означает обратное движение кометы по орбите с наклоном самой орбиты к эклиптике на 1,6º.

7. определяем параметр орбиты р:

,

где Y вычисляем с помощью непрерывной дроби:

р ≈ 2,6896 а. е.

Имея в распоряжении параметр орбиты, по очень простой формуле q=p/2 можно высчитать q (перигелийное расстояние) орбиты кометы Lulin.

q = 1,3448 а.е.

Значит, перигелий орбиты, с учетом погрешностей, находится где-то около орбиты Марса.

8. Эксцентриситет орбиты кометы Лулина, по определению равен 1, исходя из ее параболической орбиты. В связи с этим же мы не можем высчитать несуществующую большую полуось. Следовательно, такой элемент, как средняя аномалия М = 0.

9. Последним элементом находим аргумент перигелия ω. Я не нашел формул для его вычисления, поэтому мне пришлось считать аргумент перигелия и момент для прохождения (t0) перигелия с помощью специальной компьютерной программы.

В итоге вышло:

ω ≈ 152,2º

t0 ≈ 18. 01. 2009

Итак, получились такие элементы орбиты кометы С/2007 N3 Lulin:

i ≈ 178, 4º

Ω ≈ 338,8º

q ≈ 1,3448 а.е.

e = 1

M = 0

ω ≈ 152,2º

t0 ≈ 18. 01. 2009

Если сравнить с теми, что даны во Всемирной сети:

Наклон орбиты, гр 178,3704 Долгота восходящего узла, гр 338,4791Перигелийное расстояние, а.е. 1,209265

Эксцентриситет орбиты 0,999581

Аргумент перигелия, гр 136,9164

Дата прохождения перигелия 10. 01.2009 Видно, что погрешность в моих вычислениях не очень большая, даже, можно сказать, приемлемая. 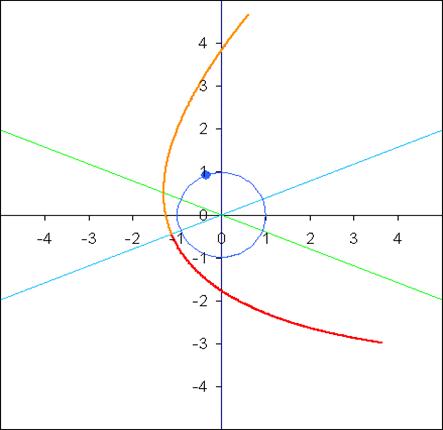Теперь, зная элементы орбиты кометы Лулина, можно начертить и саму орбиту:

ЗАКЛЮЧЕНИЕ

Таким образом, мне удалось изучить, немного пронаблюдать и сфотографировать еще одну неординарную комету C/2007 N3 (Lulin), таящую в себе много загадок. В одной из них я смог разобраться – это ее очень быстрое движение на небе среди звезд из-за нестандартного расположения орбиты кометы, но вторая – отделение хвоста – так и остается неразгаданной.

Благодаря этой комете, точнее, благодаря неблагоприятным условиям ее видимости, мне, конечно, не удалось сделать так много ее фотоснимков, как прошлых неординарных комет, но, зато на примере кометы Lulin я смог разобраться и изучить небольшой, однако, довольно непростой раздел астрометрии, такой, как вычисление кеплеровских элементов параболической орбиты, о котором раньше я знал лишь азы.

В дальнейшем я планирую подробней и более глубоко изучить комету Lulin, исходя из имеющихся данных, попытаться рассчитать ее нормальную скорость, позиционный угол хвоста и другие элементы.

СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ

1. Детская энциклопедия «Аванта» Астрономия.

2. Учебник для 11 класса Е. П. Левитан

3. Учебник для 11 класса Б. А. Воронцов-Вельяминов

4. Общий курс астрономии М. Кононович.