Расчет и коррекция исходных (априорных) кинематических поправок

Расчет кинематических поправок

Методика расчета и коррекция кинематических поправок являются наиболее разработанной процедурой цифровой обработки. Это связанно с особой важностью данной процедуры при накапливании по ОГТ.

Ввод кинематических поправок в сейсмограммы ОГТ осуществляют с целью трансформации осей синфазности однократно — отраженных волн в линии = const, где — двойное время пробега волны по лучу, нормальному к границе раздела. Выражение, определяющее кинематическую поправку для данной точки приема с абсциссой , имеет вид:

,

где — время вступления отраженной волны в точку приема с абсциссой .

,

где — эффективная скорость распространения волны до данной точки отражения; — угол наклона границы раздела.

Величина называемая фиктивной скоростью, определяет точность расчета кинематической поправки. Поскольку на начальном этапе обработки сведения о величинах и весьма приближенны, значения и определяются с погрешностями. Поэтому в практике обработки предусматриваются два этапа определения кинематических поправок.

На первом этапе рассчитывают исходные (априорные) кинематические поправки на основе априорных данных о модели среды. При этом получают грубую оценку кинематической поправки. Сейсмическая запись в расчете исходных кинематических поправок не участвует.

На втором этапе выполняют коррекцию исходных кинематических поправок с использованием сейсмограмм, базирующуюся на способах разновременного криволинейного анализа по вееру гипербол (парабол). Суть криволинейного анализа заключается в переборе значений и поиске данных, при которых максимизируется результат преобразования по заданному оператору обработки.

В результате находят либо дополнительные кинематические поправки, дающие в сумме с исходными скорректированную поправку, либо полную кинематическую поправку , обеспечивающую оптимальный эффект суммирования. Учитывая, что определение скорректированных кинематических поправок осуществляют в процессе многократного преобразования совокупности сейсмограмм с использованием достаточно сложных операторов, уже на этом начальном этапе обработки возникает необходимость в оптимальном построении алгоритма.

В большинстве сейсмогеологических ситуаций исходную кинематическую поправку рассчитывают по формуле для нормального приращения годографа ОГТ отраженной волны в однородной среде с горизонтальными границами раздела:

;

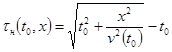здесь либо эффективная , либо средняя скорость.

Различие междуи искомой величиной определяется разницей между принятой для расчета скоростью и скоростью . В реальных условиях на скорость оказывает влияние угол наклона, слоистость среды и криволинейность границы. Недостаточное знание всех этих характеристик и особенностей их изменения по линии профиля приводит к погрешностям определения кинематических поправок.

Функцию обычно задают в виде ломаной линии значениями и в узловых точках. Значения для промежуточных времен определяют на основе линейной интерполяции. Поэтому интервалы выбирают из условия, при котором погрешность расчета исходной кинематической поправки на крайнем канале , обусловленная погрешностью , не превышает шага квантования . Такое задание априорной информации о скоростях применяют после коррекции кинематических поправок, когда найдены оптимальные значения кинематической поправки растет с увеличением абсциссы точки приема и обычно убывает с ростом . Поскольку на практике сейсмограмма представляет собой совокупность отсчетных значений, заданных с шагом квантования кинематическую поправку также рассчитывают с заданным шагом. Поэтому интервалы между изломами кривой выбирают из условия, при котором погрешность расчета , обусловленная отклонением реальной кривой от аппроксимирующей ее прямой, не превышает шага квантования . Иногда исходные кинематические поправки рассчитывают с использованием более сложных моделей сред. При этом рассматривают как нормальное приращение годографа, т. е. условие предполагают справедливым.