Страница
6
Графиков по 1-му и 2-му варианту показаны на рисунке №4 и №5 (прилагается).
5. Интегральные (календарные) кривые стока и отдачи.
Разностная интегральная (суммарная) кривая характеризует последовательный ход изменений величин ∑ (Wp-U) во времени, т.е. ∑( Wp-U) =f(T) или ∑Wp-∑U =f(T). Для построения разностной интегральной кривой вычисление производится по таблице №5.
Разностная суммарная кривая имеет следующие свойства:
1) если Wp >U – кривая идет вверх, период избытков;
2) если Wp <U – кривая идет вниз, период недостатков;
3) если Wp =U – кривая имеет перегиб, переход от избытков к недостаткам и наоборот (при многотактной работе водохранилища).
Полезный объем водохранилища по разностной суммарной кривой, исходя из ее свойств, определяется как наибольшее из вертикальных расстояний между предыдущей наивысшей и последующей наинизшей точками (рис. 6).
График работы водохранилища по 1-му варианту строится так: из каждой точки перегиба проводят вниз вертикальные (вспомогательные) линии; от начала координат (от нуля) откладывают ординату, равную Vплз, и от этой точки проводят горизонтальную линию до пересечения с первой вертикальной линией.
Точка пересечения горизонтальной линии с разносной суммарной кривой дает начало первого сброса, а пересеченье с вертикалью – конец его. В период сброса водохранилище стоит наполненным до Ннпу.
С первой точки перегиба проводят горизонтальную линию до второй вертикали. Пересечение этой линии с разностной суммарной кривой дает начало второго сброса.
От первой (а также от второй в зависимости от такта работы водохранилища) точки перегиба откладывают вниз Vплз и находят период заполнения водохранилища.
Начало сработки водохранилища соответствует концу сброса. Объемы сбросов равны их конечным ординатам.
Полная интегральная (суммарная) кривая характеризует последовательный ход изменений объемов стока во времени, строиться по уравнению W=![]() ,
,
а при ступенчатом графике W=![]() .
.
Любая i-я ордината суммарной кривой представляет собой объем воды, притекающий от начала расчетного периода до момента ti.
На рисунке 7 построена полная суммарная кривая притока ![]() Wp=f(T) и полная суммарная кривая отдачи
Wp=f(T) и полная суммарная кривая отдачи ![]() U=f(T) по данным таблицы №5.
U=f(T) по данным таблицы №5.
Основные свойства полной суммарной кривой:
1. Если Q=const, то суммарная кривая – прямая линия.
2. При ступенчатом гидрографе суммарная кривая – ломаная линия.
3. Тангенс угла наклона к оси абсцисс, касательной, проведенной к суммарной кривой в данной точке параллельно кривой отдачи – расход в данный момент, тангенс угла наклона секущей (или звена ломаной линии) – средний расход за данный период.
Полезный объем водохранилища по способу полной суммарной кривой определяется как наибольшее вертикальное расстояние между предыдущими верхними и последующими нижними касательными ![]() Wp=f(T) параллельно кривой потребления
Wp=f(T) параллельно кривой потребления ![]() U=f(T) при условии, что верхняя касательная не пересекает суммарную кривую до точки нижнего касания. Всегда сначала по ходу времени должно быть верхнее касание, а затем нижнее.
U=f(T) при условии, что верхняя касательная не пересекает суммарную кривую до точки нижнего касания. Всегда сначала по ходу времени должно быть верхнее касание, а затем нижнее.
Построение графика работы водохранилища по 2-му варианту регулирования с момента, когда V =0, т.е. от крайней правой точки кривой ![]() W проводим влево нижнюю касательную, параллельную кривой
W проводим влево нижнюю касательную, параллельную кривой ![]() U и до пересечения с кривой
U и до пересечения с кривой ![]() W. Эта точка будет соответствовать концу сброса и началу наполнения (рисунок 7).
W. Эта точка будет соответствовать концу сброса и началу наполнения (рисунок 7).
Сокращенная интегральная (суммарная) кривая строится по уравнению
W/=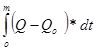 ,
,
где Qо – некоторый постоянный расход (рис. 8).
В работе в качестве постоянного расхода принимаем среднемесячный приток
Wср=Qср*t=![]() = 228,02 млн.м3.
= 228,02 млн.м3.
Ординаты сокращенной суммарной кривой притока W/=![]()
(графа 10, таблицы №5).
Ординаты сокращенной суммарной кривой потребления:
U/=![]() (графа 11).
(графа 11).
Полезный объем и график работы определяется по тому же правилу, что и для полной суммарной кривой.
| Данные для построения суммарных кривых стока и отдачи (Объем стока и отдачи в млн. м. куб.) | |||||||||||
|
Таблица №5 | |||||||||||
| Месяцы | W | U |
|
| K суммаU | Сумма W-сумма U | суммаW-KсуммаU | суммаWср | суммаW-суммаWср | суммаU-суммаWср | KсуммаU-суммаWср |
| 1 | 2 | 3 | 4 | 5 | 6 | 7=(4)-(5) | 8=(4)-(6) | 9 | 10=(4)-(9) | 11=(5)-(9) | 12=(6)-(9) |
|
|
|
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| IX | 128,36 | 40,00 | 128,36 | 40,00 | 118,97 | 88,36 | 9,39 | 228,00 | -99,64 | -188,00 | -109,03 |
| X | 105,75 | 40,00 | 234,11 | 80,00 | 237,94 | 154,11 | -3,83 | 456,04 | -221,93 | -376,04 | -218,10 |
| XI | 115,75 | 40,00 | 349,86 | 120,00 | 356,91 | 229,86 | -7,05 | 684,06 | -334,20 | -564,06 | -327,16 |
| XII | 125,99 | 40,00 | 475,85 | 160,00 | 475,87 | 315,85 | -0,02 | 912,09 | -436,24 | -752,09 | -436,21 |
| I | 125,99 | 40,00 | 601,84 | 200,00 | 594,84 | 401,84 | 7,00 | 1 140,11 | -538,27 | -940,11 | -545,27 |
| II | 92,29 | 40,00 | 694,13 | 240,00 | 713,81 | 454,13 | -19,68 | 1 368,13 | -674,00 | -1 128,13 | -654,32 |
| III | 125,99 | 40,00 | 820,12 | 280,00 | 832,78 | 540,12 | -12,66 | 1 596,16 | -776,04 | -1 316,16 | -763,38 |
| IV | 144,44 | 40,00 | 964,56 | 320,00 | 951,75 | 644,56 | 12,81 | 1 824,18 | -859,62 | -1 504,18 | -872,43 |
| V | 1 190,78 | 150,00 | 2 155,34 | 470,00 | 1 397,88 | 1 685,34 | 757,46 | 2 052,20 | 103,14 | -1 582,20 | -654,32 |
| VI | 293,81 | 150,00 | 2 449,15 | 620,00 | 1 844,01 | 1 829,15 | 605,14 | 2 280,23 | 168,92 | -1 660,23 | -436,21 |
| VII | 154,31 | 150,00 | 2 603,46 | 770,00 | 2 290,15 | 1 833,46 | 313,31 | 2 508,25 | 95,21 | -1 738,25 | -218,10 |
| VIII | 132,82 | 150,00 | 2 736,28 | 920,00 | 2 736,28 | 1 816,28 | 0,00 | 2 736,27 | 0,01 | -1 816,27 | 0,01 |
| ИТОГО: | 2 736,28 | 920,00 | 14 213,06 | 4 220,00 | 12 551,20 | 9 993,06 | 1 661,86 | 17 785,72 | -3 572,66 | -13 565,72 | -5 234,53 |
|
К= |
|
= |
2,97 |
Wср= |
228,02 | ||||||
