а при α < βi:

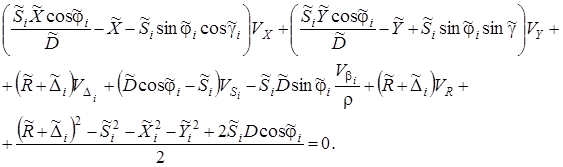(23)

Введем обозначения: при α > βi:

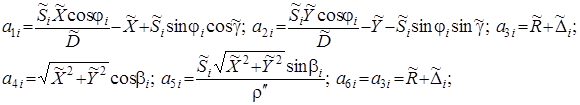
при α < βi:

остальные коэффициенты остаются без изменений.

С учетом принятых обозначений условные уравнения примут вид:

. (24)

Измеренные значения углов βi и расстояний от дальномера до стенок тоннеля Si, представлены в табл.1.

Зная проектное значение радиуса тоннеля R = 255 см, высоту пола h1 и высоту инструмента h2, можно вычислить приближенное значение величины

: .

В нашем случае h1 + h2 = 232 см, следовательно, = 23 см. В соответствии с ранее принятым расположением осей координат, величину вычислим по горизонтальным расстояниям S1 и S7:

. (25)

Из табл.1 находим, что S1=188,5 см, S7=318,0 см, следовательно,

=64,8 см.

По приближенным координатам оси инструмента вычисляется угол :

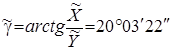и углы .

Затем вычисляются коэффициенты аij. по приведенному выше алгоритму.

Известно, что деформации колец тоннеля – величины сравнительно малые, и в первом приближении примем со средней квадратической ошибкой 3 – 4 см. На примере расчета далее показано, что такой подход позволяет вычислить необходимые деформационные характеристики, однако у него имеются и некоторые недостатки. При уравнивании результатов измерений подобных схем измерений под условием (8), поправки к приближенным отклонениям фактического положения стенок тоннеля от окружности, по сути, являются собственно отклонениями, так как принято, что . Далее рассмотрен иной подход к обработке результатов измерений.

По приближенным координатам оси инструмента вычислим угол

: и углы, которые отражены в табл.1 (φi).

Найдем невязки li по формуле:

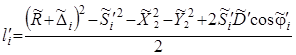и затем представим их в виде матрицы L.

Составим матрицу обратных весов, используя средние квадратические ошибки, , где элементами симметричной диагональной матрицы М размером 24×24 являются следующие средние квадратические ошибки: mx,y = 3 см, mΔ= 3 см, mS = 0,3 см, mβ = 20", mR = 3 см.

Вектор коррелат рассчитывается по формуле:

.

Вектор поправок найдем по формуле: .

Известно, что деформации колец тоннеля – величины сравнительно малые, и в первом приближении примем Δi = 0 со средней квадратической ошибкой 3 – 4 мм. Получив поправки V, можно найти фактическое положение стенок и радиуса тоннеля, по формулам (15). В итоге получен вектор поправок Vi (поправки в линейные величины выражены в сантиметрах, а в угловые – в секундах). После определения поправок в измеренные величины, найдено фактическое положение стенок и радиус тоннеля по формуле (15). (Численные значения в автореферате не приводятся).

Выполненный анализ точности результатов уравнивания показал, что величины деформаций колец тоннеля получены со средней квадратической ошибкой 3 мм, а координаты реального положения оси тоннеля – со средней квадратической ошибкой 1,9 мм, как и величина вероятнейшего радиуса.

Далее в диссертации разработан второй метод определения деформаций стенок тоннеля с одновременным вычислением вероятнейшей окружности. В данном методе рассмотрены результаты измерений полярных координат (углов и расстояний) с одной стоянки электронного тахеометра. В данном случае целесообразно представить функцию (10) в следующем виде:

. (26)

Равенство (26) будет удовлетворено лишь в случае, если все величины будут уравнены.

Измеренные величины представим в виде:

где волнистой чертой сверху отмечены измеренные, либо приближенно известные величины.

Величины деформаций в первом приближении известны , как величины малые, следовательно, поправки к ним будут собственно смещениями наблюдаемых точек от вероятнейшей кривой: .

Представим величины, характеризующие положение вероятнейшей окружности, в виде

где величины являются дополнительными неизвестными. В таком случае уравнение (26) имеет вид: