Формулы вычисления углов наклона для теодолитов 2Т30 имеют следующий вид: (3)

Где МО = 0,5 (Л + П). (4)

Теодолиты 2Т5 и 2Т5К.

 Теодолит 2Т5 (2Т5К), точный оптический прибор предназначен для измерения горизонтальных и вертикальных углов в триангуляции и полигонометрии 1 и 2 разрядов, для измерения расстояний с использованием нитяного дальномера. Оптический теодолит 2Т5 (рис. 3, стр 8) имеет следующие основные особенности. Система вертикальной оси не повторительная; отсчет по угломерным кругам производится по одной стороне круга; оцинковка вертикального круга выполнена по секторам от 0 до 75° и от 0 до - 75° и др. Зрительная труба обоими концами переводится через зенит. Между корпусом трубы и осью расположено клиновое кольцо 3 (рис. 3, стр 8), вращением которого изменяют направление визирной оси зрительной трубы относительно горизонтальной оси при устранении коллимационной погрешности. Для установки прибора над точкой местности теодолит снабжен оптическим центриром. Уровень при алидаде вертикального круга расположен в левой колонке прибора. Изображение его пузырька, освещаемое через окно 7, передано на повторную призму – лупу 6.Юстируют уровень двумя винтами, закрытыми пробкой. При измерении углов наклона концы пузырька совмещают установочным винтом. Поле зрения отсчетного микроскопа теодолита показано на рис 5. Для вычисления углов наклона и места нуля используют формулы (3) и (4).

 Теодолит 2Т5К (рис. 4, стр 8) в отличии от теодолита 2Т5 снабжен самоустанавливающимся оптическим компенсатором, заменяющим уровень при алидаде вертикального круга и позволяющим использовать прибор в качестве нивелира[1] с горизонтальным лучом визирования.

 теодолит 2Т5КП в отличии от 2Т5К снабжен зрительной трубой прямого изображения. Изображения одного деления угломерного круга (рис. 5, стр 8) должно быть равно 60 делениям шкалы микроскопа. Рен горизонтального круга определяют также, как у теодолита 2Т30, через 60°, а рен вертикального круга – на участках 0; 2° - 2° при круге слева и справа. Расхождения между значениями рена на различных участках круга недолжно превышать 0,2¢ (12²).

Рисунок 1. Теодолит Т30.

1 – наводящий винт горизонтального круга; 2 – окуляр микроскопа; 3 – зеркало; 4 – цилиндрический уровень на зрительной трубе; 5 – закрепительный винт зрительной трубы; 6 – наводящий винт зрительной трубы; 7 – окуляр зрительной трубы; 8 – наводящий винт алидады; 9 – подъемный винт.

Рисунок 2.

Поле зрения отсчетного микроскопа теодолита 2Т30.

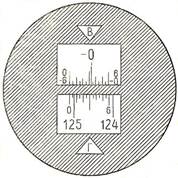Отсчет по горизонтальному кругу 125° 06,5¢: отсчет по вертикальному кругу - 0° 26¢.

Рисунки 3 и 4.

Теодолиты 2Т5, 2Т5К.

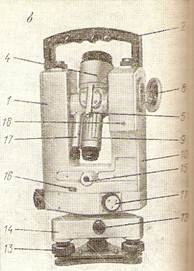3 – 2Т5; 4 – 2Т5К. 1 – колонка; 2 – ручка; 3 – клиновое кольцо; 4 – зрительная труба; 5 – коллиматорный визир; 6 – призма луча; 7 – окно; 8 – зеркало; 9 – кремальера; 10 – боковая крышка; 11 – рукоятка перевода горизонтального круга; 12 – закрепительный винт подставки; 13 – подъемный винт; 14 – подставка; 15 – окуляр; 16 – иллюминатор круга искателя; 17 – микроскоп; 18 – юстировочный винт для приведения МО к нулю.

Рисунок 5. Поле зрения отсчетного микроскопа теодолитов 2Т5, 2Т5К, 2Т5КП.

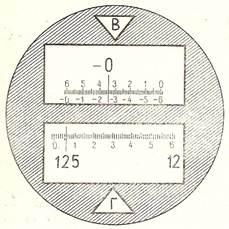Отсчет по горизонтальному кругу 125° 05,4¢; отсчет по вертикальному -0° 25,0¢.

Рисунок 6.

Поле зрения отсчетного микроскопа теодолита Т30.

Отсчет по горизонтальному кругу 70° 0,5¢; отсчет по вертикальному кругу 358° 48¢.

Измерение и построение горизонтальных углов

 Построение углов на местности при помощи ленты

Произведя соответствующие расчеты, можно при помощи ленты решать и обратную задачу – строить на местности углы заданной величины. Пусть требуется построить угол, равный 37°30¢. Так этому углу соответствует хорда 6,43м, тем самым построим данный угол. Он будет заключен между десяти метровыми сторонами. Точно также вместо десятиметровых сторон можно откладывать другие, например 5 или 20м, но в этом случае в соответствующее число раз надлежит уменьшать или увеличивать значение хорды (в данном случае в 2 раза).

Изложенный прием, основанный на использовании таблицы хорд, может быть с успехом применен и при построении (измерении) углов на плане.

При выполнении топографических работ все чаще встречается необходимость в построении прямого угла 90° и угла 45°. Построение этих углов можно выполнять и без таблицы хорд.

На (рис. 7, стр. 11) показано построение прямого угла в точке С к стороне АС. Это построение основано на том, что в треугольнике со сторонами 3; 4 и 5 м угол, лежащий против пятиметровой стороны, - прямой угол (90°).[2] Для получения большей точности, стороны этого треугольника могут быть увеличены в любое число раз.

Аналогичным образом может быть построен прямой угол при помощи треугольника со сторонами 5,00; 7,07; и 5м. на этот раз углы против 5,00м сторон будут равны 45°, а против 7,07м - 90°.

Кроме того для построения угла в 45° можно использовать треугольник со сторонами 7,00; 4,00; и 5,04м или 7,00; 6,00; и 5,06м, в которых угол в 45° будет лежать опять против пятиметровой стороны.

Рисунок 7. Использование длин сторон треугольника: построение треугольника.

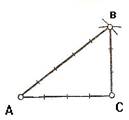С большей точностью угол в 45° может быть построен по треугольнику 17; 17; и 13м, здесь он будет лежать против стороны 13м[3].

 Построение углов с помощью экера

Экер – специальный прибор для построения прямых углов. Простейший экер крестообразный; состоит из кола и двух планок, на каждой из которых вбито отвесно по две иголки. Иголки расположены таким образом, что соединяющие их линии пересекаются под прямым углом.