Очевидно, что для определения элементов взаимного ориентирования необходимо измерить на стереопаре снимков не менее 5 точек.

В качестве примера рассмотрим определение элементов взаимного ориентирования by, bz, w2’, a2’, À2’.

В связи с тем, что уравнения ( 4.3) не линейны, их предварительно приводят к линейному виду и переходят к уравнению поправок:

. ( 1)

В уравнении поправок коэффициенты ai частные производные от функции ( 4.3) по соответствующим аргументам, а ℓ– свободный член.

Значения коэффициентов аi в уравнении ( 1) вычисляют по следующим известным значениям:

– измеренным координатам точек на стереопаре снимков – хi, yi;

– элементам внутреннего ориентирования снимков fi, x0i, y0i;

– 3 параметрам, задающим ориентацию системы координат модели (в нашем случае w1’, a1’, À1’) и приближенным значениям элементов взаимного ориентирования.

Свободный член ℓ вычисляется по формуле ( 4.3) таким же образом.

Полученную систему уравнений поправок решают методом приближений, а в случае, если измерено более 5 точек по методу наименьших квадратов (под условием VTPV=min). В результате решения находят значения элементов взаимного ориентирования.

Критерием, по которому принимается решение о завершении итерраций, могут являться величины поправок к определяемым неизвестным или величины остаточных поперечных параллаксов, которые для каждой измеренной точки вычисляются по формулам:

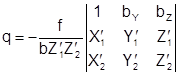; ( 2)

где .

Величина qост представляет собой разность ординат измеренных точек на стереопаре снимков, приведенных к идеальному случаю съемки, то есть q=y1-y2.

Необходимо отметить, что при отсутствии ошибок построения снимка и ошибок измерений величина q должна быть равна 0.

При определении элементов взаимного ориентирования оптимальным вариантом считается измерение 12-18 точек на стереопаре снимков, расположенных парами или тройками в 6 стандартных зонах (рис. 1).

- главная точка снимка

- стандартно расположенная зона

В этом случае получается наиболее точное и надежное определение элементов взаимного ориентирования и появляется возможность локализации грубых измерений.

6. Построение фотограмметрической модели

Построение фотограмметрической модели заключается в определении координат точек объекта по измеренным на стереопаре снимков координатам их изображений в системе координат модели ОМХМYMZM.

Определение координат точек модели производится по формулам прямой фотограмметрической засечки (см. раздел 1).

При этом координаты центра проекции S принимаются произвольными (обычно 0). Также произвольно (но не равной 0) выбирается величина ВХ. В большинстве случаев практики величину ВХ принимают равной:

;

где b – базис фотографирования в масштабе снимка,

m – знаменатель масштаба снимка.

Остальные значения элементов внешнего ориентирования определяют по 8 параметрам by, bz, w1’, a1’, À1’, w2’, a2’, À2’, 5 из которых являются элементами взаимного ориентирования, а 3 определяют ориентацию системы координат модели.

При этом

.

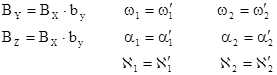Например, если были определены элементы взаимного ориентирования a1’, À1’, w2’, a2’, À2’ и при этом величины параметров by, bz, w1’ были приняты равными нулю (by=bz=w1’=0), то BY=BZ=0, w1=0, a1=a1’, À1=À1’, w2=w2’, a2=a2’, À2=À2’.

Если были определены элементы взаимного ориентирования by, bz, w2’, a2’, À2’, а величины параметров w1’, a1’, À1’ были приняты равными нулю (w1’= a1’= À1’=0), то

.

7. Внешнее ориентирование модели. Элементы внешнего ориентирования модели

На рис.1: OXYZ - система координат объекта, ОМХМYMZM - система координат фотограмметрической модели , А – точка объекта ,АМ -точка фотограмметрической модели, соответствующая точке А объекта .

Векторы определяют положение начала системы координат модели ОМХМYMZM и точки А местности относительно начала системы координат объекта OXYZ.

Векторы определяют соответственно положение точек АМ и А относительно системы координат фотограмметрической модели.

Из рис. 1 следует, что

. ( 1)

Векторы коллинеарны, поэтому

; ( 2)

где t – знаменатель масштаба модели.

С учетом ( 2) выражение ( 1) имеет вид:

; ( .3)

В координатной форме выражение ( 3) имеет вид:

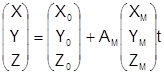; ( 4)

Или

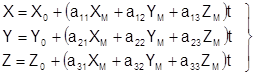. ( .5)

В выражениях ( 4) и ( 5):

X, Y, Z – координаты точки объекта в системе координат объекта;

ХМ, YM, ZM - координаты соответствующей точки модели в системе координат фотограмметрической модели;

АМ – матрица преобразования координат, элементы aij которой являются функциями углов wМ, aМ, ÀМ, определяющих ориентацию системы координат модели относительно системы координат объекта;

t – знаменатель масштаба модели.

7 параметров: - называют элементами внешнего ориентирования модели.

8. Определение элементов внешнего ориентирования модели по опорным точкам

Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения ( 7.5), которые представим в виде:

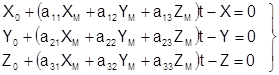. ( 1)