1.4 Оценка точности полевых измерений

Качество полевых измерений оценивается по средней квадратической ошибке измерения угла. Средняя квадратическая ошибка единицы веса вычисляется по формуле:

,

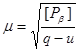где q – число звеньев в сети, u – число узловых точек. Тогда μ=3,9.

Средние квадратические ошибки ошибки μx и μy единицы веса абсцисс и ординат:

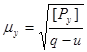
1.5 Оценка точности уравненных значений координат узловой точки

Определяют средние квадратические ошибки уравновешенных координат узловой точки:

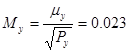
Определяют средние квадратические ошибки уравненного значения дирекционного угла

Рассмотренная оценка точности координат при раздельном уравнивании сети – приближённая, так как она производится не по строгим формулам теории ошибок.

1.6 Вычисление весов и координат узловой точки

Веса вычисляют по формулам:

,

Где

В данных формулах:

μ – коэффициент влияния случайных ошибок линейных измерений (μ= 0.0005)

L – расстояние между начальной и узловой точкой

θ – дирекционный угол замыкающей линии

n – число сторон в ходе

Тогда средневесовые значения координат узловой точки равны:

1.7 Оценка точности вычисления координат узловой точки

Оценка точности уравненных координат узловой точки выполняется по формулам, приведённым в разделе 1.5. Результаты определения весов узловой точки записывают в таблицу 6.

Таблица 6 – Ведомость вычисления весов узловой точки