Гидравлический расчет узла гидротехнических сооружений
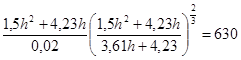
Решив это уравнение найдем:
h=1,72 м ω=1,5h2+4,23h=11,68м2.
Изменяем уклон дна, для этого в начале канала сделаем одноступенчатый перепад.
 |
i=0,00015
Решив это уравнение найдем:
h=1,5 м b=3,38h=5,1 м.
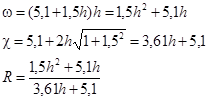
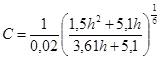
Решив это уравнение найдем:
h=2,06 м ω=1,5h2+5,1h=16,81м2.
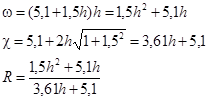
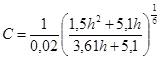
Решив это уравнение найдем:
h=1,29 м ω=1,5h2+5,1h=9,04 м2 R=0,93 м.
1.2 Расчет канала гидравлически наивыгоднейшего сечения
Гидравлически наивыгоднейшее сечение – такое, у которого при заданных ω, i расход Q оказывается максимальным.
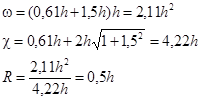
Решив это уравнение найдем:
h=3,01 м b=0,61h=1,84 м.
1.3 Определение нормальных глубин для заданных расходов Qmin, Q, Qmax и построение кривой Q=f(h)
i=0,00015
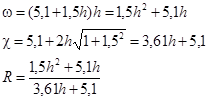
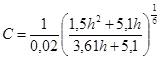
Вычисления удобно свести в таблицу:
|
Q, м3/с | ||
|
0 |
0 | ||
|
0,5 |
1,0037 | ||
|
1 |
3,3392 | ||
|
1,5 |
6,9297 | ||
|
2 |
11,847 | ||
|
2,5 |
18,188 | ||
|
3 |
26,059 | ||
|
3,5 |
35,566 | ||
|
4 |
46,814 | ||
|
4,5 |
59,907 | ||
|
5 |
74,946 |
По графику можно определить нормальные глубины для заданных расходов.
1.4 Определение типа и построение кривой свободной поверхности
При проведении гидравлических расчетов неравномерного движения, например, при расчете кривых свободной поверхности, сопряжении бьефов, необходимо знать критическую глубину hкр. Критическая глубина соответствует минимуму удельной энергии сечения и в общем случае определяется из уравнения:
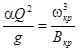
α ≈1
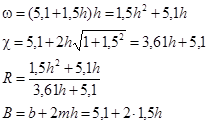
Решив это уравнение найдем:
Критический уклон найдем по формуле:
– обычный канал.
Тип кривой аI, кривая подпора.
Построение кривой свободной поверхности:
 |
|
