S2.

A2.

R2.

C2.

S2. - Вычисление В-сплайна нулевой степени.

A2. - Х - координата функции по оси абсцисс.

C2. - ограничения имеют вид:

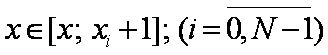
T2. - В-сплайн нулевой степени.

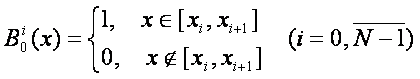
R2. - В-сплайн нулевой степени.

Логическая ячейка 3.

S3.

A3.

R3.

C3.

S3. - Получение нового разбиения и для него рекуррентное соотношение.

A3. - Входные данные x, xi, xi+n, xi+1, xi+n+1, Bin-1(x).

C3. - Новое разбиение ,

(x-n<x-n+1<…<x-1<x0<x1<…<xN<xN+1<…<xN+n),

n=1,2,…; ;

T3. - Рекуррентное соотношение.

R3. - Bin(x) –рекуррентное соотношение на выходе ячейки.

Логическая ячейка 4.

S4.

A4.

R4.

C4.

S4. - Хранение предыдущего значения сплайна Bin-1(x).

A4. - Предыдущее значение сплайна Bin-1(x).

M4. - Модуль хранения значения со входа ячейки.

T4. - Передача хранимого значения на выход.

R4. - Предыдущее значение сплайна Bin-1(x).

Логическая ячейка 5.

S5.

A5.

R5.

C5.

S5. - Вычисление В-сплайна третей степени Bi3(x).

A5. - t -размер шага движения по оси абсцисс.

C5. - ограничения:

; x < xi-2;

xi-2 < x < xi-1;

xi-1 < x < xi;

xi < x < xi+1;

xi+1 < x < xi+2;

xi+2 < x.

T5. - Выражение В-сплайна третей степени.

R5. – Выражение В-сплайна третей степени Bi3(x).

Логическая ячейка 6.

S6.

A6.

R6.

C6.

S6. - Вычисление В-сплайна пятой степени Bi5(x).

A6. - t -размер шага движения по оси абсцисс.

C6. - ограничения:

; x < xi-3;

xi-3 < x < xi-2;

xi-2 < x < xi-1;

xi-1 < x < xi;

xi < x < xi+1;

xi+1 < x < xi+2;

xi+2 < x < xi+3;

xi+3 < x.

T6. - Выражение В-сплайна пятой степени.

R6. - Выражение В-сплайна пятой степени Bi5(x).

Логическая ячейка 7.

S7.

A7.

R7.