Математическое моделирование технологического процесса изготовления ТТЛ-инвертораРефераты >> Технология >> Математическое моделирование технологического процесса изготовления ТТЛ-инвертора
Введение
1Расчет режимов технологического процесса и распределение примесей после диффузии
1.1 Распределение примесей в базе
1.2 Расчет режимов базовой диффузии
1.3 Распределение примесей в эмиттере
1.4 Расчет режимов эмиттерной диффузии
2 Расчет слоевых сопротивлений биполярного транзистора
3 Расчет основных параметров инвертора
Заключение
Список используемой литературы
Введение
Развитие микроэлектроники и создание новых БИС и СБИС требует новых методов автоматизированного проектирования, основой которого является математическое моделирование всех этапов разработки микросхемы.
Необходимость внедрения гибких систем автоматизированного проектирования очевидна, поскольку проектирование микросхем сложный и длительный процесс. В настоящее время используется сквозное моделирование микросхем, которое включает в себя расчет и анализ характеристик и параметров на следующих уровнях:
-технологическом;
-физико-топологическом;
-электрическом;
-функционально-логическом.
В ходе данной работы нам необходимо осуществить сквозное проектирование схемы ТТЛ-инвертора на трех первых уровнях.
Расчеты предусматривается произвести с использование программы расчета параметров модели биполярного транзистора Biptran и программы схемотехнического моделирования PSpice.
1Расчет режимов технологического процесса и распределение примесей после диффузии
1.1 Распределение примесей в базе
Распределение примесей в базе описывается кривой Гаусса и определяется формулой:
 , (1)
, (1)
где: NS- поверхностная концентрация акцепторов;
D- коэффициент диффузии примеси;
t- время диффузии;
![]() - глубина залегания коллекторного p-n перехода.
- глубина залегания коллекторного p-n перехода.
Поверхностная концентрация определяется по формуле:
 , (2)
, (2)
Из формулы 1 выражаем D2t2:
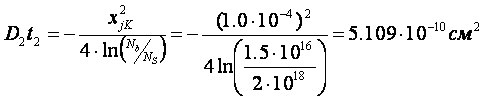
Тогда имеем следующее выражение для распределения примеси в базе:
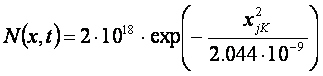 , (3)
, (3)
Результаты расчета распределения примеси в базе приведены в таблице 1, а сама кривая представлена на рисунке 1.
1.2 Расчет режимов базовой диффузии
К основным параметрам диффузионного процесса относят время диффузии и температуру диффузии.
Из выражения 2 найдём произведение D1t1 для первого этапа диффузии (загонки) по формуле:
|
где ![]()
В результате получим:
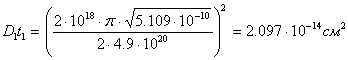
Коэффициент диффузии примеси определяется из выражения Аррениуса:
|
где ![]() =5.1 (для бора) – постоянная диффузии,
=5.1 (для бора) – постоянная диффузии,
![]() =3.7 (для бора) – энергия активации,
=3.7 (для бора) – энергия активации,
k – постоянная Больцмана,
Т – температура процесса диффузии.
Таким образом для бора получаем следующее выражение:
|
Температуру базовой диффузии при загонке выберем равной 1073К (800°С), а при разгонке 1373К (1100°С) тогда:
![]()
![]()

![]()
1.3 Распределение примесей в эмиттере
Эмиттерную диффузию ведут в одну стадию и распределение примеси описывается erfc-функцией:
|
(5)
где ![]() - концентрация предельной растворимости мышьяка в кремнии при заданной температуре (1100°С);
- концентрация предельной растворимости мышьяка в кремнии при заданной температуре (1100°С);
![]() - глубина залегания эмиттерного p-n перехода.
- глубина залегания эмиттерного p-n перехода.
Диффузия мышьяка идёт в неоднородно легированную базовую область, поэтому расчётная формула усложняется:
|
(6)
где![]() при 1100°С;
при 1100°С;
![]() .
.
Подставив эти значения в выражение 6 получим: ![]() .
.
Подставляя это значение в выражение 5 получим распределение мышьяка в эмиттерной области после диффузии. График распределения представлен на рисунке 1.
1.4 Расчет режимов эмиттерной диффузии
Найдём, по аналогии с базовой диффузией, для эмиттерной время и температуру процесса. В данном случае температура процесса задана (1100°С) и необходимо найти только время диффузии. Для этого необходимо сначала определить коэффициент диффузии, который находится из выражения 4. Постоянная диффузии D0 энергия активации ![]() для фосфора равны 10,5 и 4,08 соответственно. Тогда получаем:
для фосфора равны 10,5 и 4,08 соответственно. Тогда получаем:

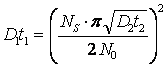
 , (4)
, (4)