Цена и объем производства в условиях монополии и олигополической конкуренцииРефераты >> Экономическая теория >> Цена и объем производства в условиях монополии и олигополической конкуренции
Рис. 6. Ломаная кривая спроса
Предположим, что у фирмы цена за единицу продукта ОР, а объем продаж OX (рис. 6а), DEF – кривая спроса на товары фирмы. Она принимает решпние повысить цену на свои товары. Новая цена ОР1 . Другой вариант: она понижает цену до ОР2 . Предположим далее, что соперники следуют за фирмой при установлении цен. В таком случае GEH представляла бы кривую спроса фирмы, совпадающую с кривой спроса ее соперников. На практике же, если фирма поднимает цену, соперники не следуют за ней и не повышают цену, с тем чтобы увеличить свою долю рынка за счет фирмы. Если фирма понижает цену, соперники реагируют на такое сокращение, с тем чтобы предотвратить потерю своей доли рынка. Таким образом, завершающая кривая спроса составляется из двух сегментов DE и EH с переломом в точке Е. Сотрем отрезки GE и EF и получим ломаную кривую спроса в данной отрасли DEH (рис. 6б). Фирмы не реагируют на повышение цен и снижают цены вслед за снижением цен одной из них.
При высокой рыночной концентрации ценовые решения продавцов взаимозависимы. Олигополистические фирмы исходят из того, что прибыли будут выше, когда проводится общая политика, чем когда каждая фирма преследует свои узкоэгоистические интересы. В олигополистических отраслях действует тенденция в направлении к коллективным действиям, приближая ценовое поведение к чистой монополии.
Фирмы, действующие в рамках олигополистической структуры ранка, стремятся к созданию системы связей, которая позволила бы координировать поведение в общих интересах. Одной из форм такой координации является так называемое лидерство в ценах. Оно состоит в том, что изменения в справочных ценах объявляются определенной фирмой, которая признается лидером всеми остальными, следующими в ценовой политике за ней.
5.2. Модель Курно
Предположим, что обе фирмы (А и Б) производят однородный товар и знают кривую рыночного спроса на него. Каждая фирма должна решить, сколько продукции выпускать, и обе фирмы принимают свои решения одновременно и независимо друг от друга. При принятии решений каждая из двух фирм исходит из того, что ее конкурент тоже принимает решения по объему производства и что конечная цена будет зависеть от совокупного объема производства обеих фирм. Условием модели является также предположение о постоянном объеме производства конкурента, на основе чего принимается собственное решение по объему выпуска.
Чтобы увидеть, как это происходит, рассмотрим решение по объему производства, принимаемое фирмой А. Допустим, фирма А считает, что фирма Б ничего производить не будет. Тогда ее кривая спроса полностью совпадает с кривой рыночного спроса D1 (0). При этом предельный доход будет изображать кривая VR1(0) (рис. 7).
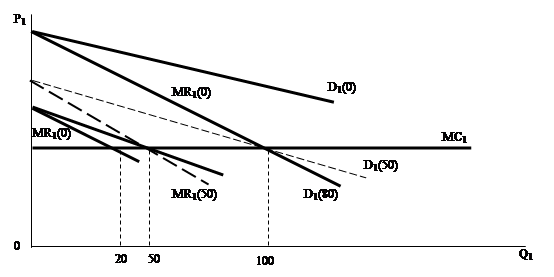
Рис. 7. Оптимизация объема производства фирмы А в зависимости от объема производства фирмы Б.
Как видно на графике, фирма А будет максимизировать прибыль при объеме 50 единиц, так как именно в этом случае предельный доход IR1(0) сравняется с предельными издержками MC1 . Следовательно, если фирма Б ничего не производит, фирма А будет выпускать 50 единиц товара.
Если фирма А считает, что фирма Б выпускает 50 единиц, тогда кривая спроса фирмы А представляет собой кривую рыночного спроса, смещенную влево на 50 единиц. На рис. 7 это отмечено как D1(50), чему соответствует кривая предельного дохода IR1(50). В этом случае максимизирующий прибыль объем производства фирмы А равен 25 единиц (точка, где IR1(50) = MC1).
Предположим, что фирма А рассчитывает, что фирма Б будет производить 75 единиц, тогда новая кривая спроса фирмы А будет D1(75) . Теперь максимизирующий прибыль объем производства фирмы А равен 12,5 (точка, где IR1(75) = MC1). Наконец, пусть фирма А полагает, что фирма Б производит 100 единиц, тогда кривая спроса и предельного дохода фирмы А (не показанные на графике) пересекут кривую ее предельных издержек на вертикальной оси. Если фирма А предполагает, что фирма Б будет производить 100 единиц, то фирма А не будет выпускать продукции.
|
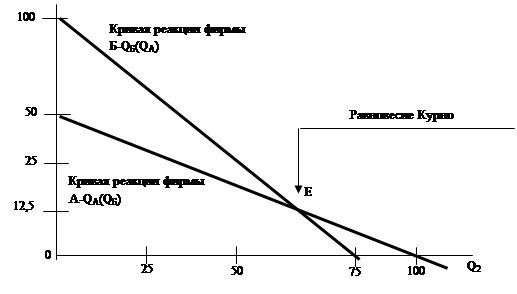 |
Рис. 8. Равновесие Курно.
На рис. 8 изображена реакция фирмы А на изменение выпуска фирмой Б. Кривая реакции фирмы А – QA(QБ) . Осуществив аналогичный анализ для фирмы Б, мы получим кривую реакции фирмы Б – QБ(QA).
Пересечение кривых реакции этих двух фирм (точка Е) показывает равновесие Курно. При таком равновесии каждая фирма правильно угадвает поведение конкурента и принимает для себя оптимальное решение. В замисимости от этого она может максимизировать прибыль.
Мы определили равновесие Курно для двух фирм. Однако оно может быть найдено и для большего числа фирм, и можно доказать в общем виде, что если
|
отрасль включает n фирм, то каждая из них будет производить | 1 | |
| n + 1 | ||
|
общего объема рынка, а все вместе они будут выпускать | 1 |
´ n |
| n + 1 |
объема рынка. Очевидно, что по мере роста числа фирм уровни цен и объемов производства будут все более приближаться к уровню, характерному для совершенной конкуренции.
Модель равновесия Курно предполагает, что фирмы-дуополисты конкурируют друг с другом. Однако ситуация принципиально изменится, если оно смогут договориться между собой и выбрать свои объемы производства на совместной, а не на конкурентной основе.
Предположим, что кривая рыночного спроса дуополистов (А и Б) описывается уравнением Р=60 – Q, где Q – совокупное производство обеих фирм (т.е. Q=QА + QБ).
Предположим также, что у обеих фирм предельные издержки равны нулю: MC1=MC2=0.
В этом случае кривая реакции фирмы А будет определяться следующим образом. Для максимизации прибыли предельные издержки фирмы должны быть равны предельному доходу. При этом общий доход фирмы А будет составлять:
RA=PQA=(60 - Q)´QA;
RA=60QA – (QA + QБ)´QA;
