Модели экономического ростаРефераты >> Экономическая теория >> Модели экономического роста
Р.Ф. Харрод построил специальную модель экономического роста (1939г.), включив в неё экзогенную функцию инвестиций (в отличие от экзогенно заданных инвестиций у Домара) на основе принципа акселератора и ожиданий предпринимателей (предпосылки модели Харрода остаются теми же, что и в модели Домара).
Согласно принципу акселератора, любой рост (сокращение) дохода вызывает рост (сокращение) капиталовложений, пропорциональный изменению дохода:
It=v(Yt-Yt-1), где v — акселератор.
Предприниматели планируют объем собственного производства, исходя из ситуации, сложившейся в экономике в предшествующий период: если их прошлые прогнозы относительно спроса оказались верными и спрос полностью уравновесил предложение, то в данном периоде предприниматели оставят темпы роста объема выпуска неизменными; если спрос в экономике был выше предложения, они увеличат темпы расширения производства; если предложение превышало спрос в предшествующем периоде, они снизят темпы роста. Формализовать это можно следующим образом:
(Yt-Yt-1)/ Yt-1=а(Yt-1-Yt-2)/ Yt-2
где а=1, если спрос в предшествующем периоде (t-1) был равен предложению; а>1, если спрос превысил предложение и а<1, если спрос был ниже предложения. Отсюда получим объём предложения в экономике:
Yt=Yt-1 {а (Yt-1-Yt-2)/ Yt-2+1}.
Для определения совокупного спроса используется модель акселератора (а также условие равенства I=S):
Yt=It/s= v(Yt-Yt-1)/s.
Равновесный экономический рост предлагает равенство совокупного спроса и предложения:
v(Yt-Yt-1)/s= Yt-1{а (Yt-1-Yt-2)/ Yt-2+1}.
После небольшого преобразования получим:
v/s {(Yt-Yt-1) /(Yt-1)} =а{(Yt-1-Yt-2)/ Yt-2}+1.
Предположим, что в предшествующем периоде спрос был равен предложению, т.е. а=1. Тогда, в соответствии с принятыми условиями поведения, предприниматели и в текущем периоде сохранят темпы роста производства такими же, как и в предшествующем периоде, т.е.
(Yt-Yt-1) /Yt-1=(Yt-1-Yt-2)/ Yt-2=ΔYt/ Yt-1.
Тогда предыдущее выражение можно представить следующим образом:
v/s (ΔYt/ Yt-1)= (ΔYt/ Yt-1) +1, отсюда равновесный темп прироста объёма выпуска составит: ΔY/ Yt-1=s/(v-s). Харрод назвал выражение s/(v-s) «гарантированным» темпом роста: поддерживая его, предприниматели будут полностью удовлетворены своими решениями, поскольку спрос будет равен предложению и их ожидания будут сбываться. Такой темп роста обеспечивает полное использование производственных мощностей (капитала), но полная занятость при этом не всегда достигается.
Анализ соотношений между гарантированным и фактическим темпами роста позволил сделать следующий вывод: если фактически запланированный предпринимателями темп роста предложения отличается от гарантированного темпа роста (превышает или не достигает его), то система постепенно отдаляется от состояния равновесия.
Помимо гарантированного темпа роста Харрод вводит понятие"естественного" темпа роста. Это максимальный темп, допускаемый ростом активного населения и техническим прогрессом.
При таком темпе достигается полная занятость факторов труда и капитала.
Если гарантированный темп роста, удовлетворяющий предпринимателей, выше естественного, то вследствие недостатка трудовых ресурсов фактический темп окажется ниже гарантированного: производители будут разочаровываться в своих ожиданиях, снизят объём выпуска и инвестиции, в результате чего система будет находиться в состоянии депрессии.
Если гарантированный темп роста меньше естественного, то фактический темп может превысить гарантированный, поскольку существующий избыток трудовых ресурсов даёт возможность увеличить инвестиции. Экономическая система будет переживать бум. Фактический темп роста может быть также равен гарантированному, и тогда экономика будет развиваться в условиях динамического равновесия, вполне удовлетворяющих предпринимателей, но при наличии вынужденной безработицы.
Идеальное развитие экономической системы достигается при равенстве гарантированного, естественного и фактического темпов роста в условиях полной занятости ресурсов.
Но поскольку всякое отклонение инвестиций от условий гарантированного темпа роста, как известно, выводит систему из равновесия и сопровождается все более увеличивающимся расхождением между спросом и предложением, динамическое равновесие в модели Харрода также оказывается неустойчивым.
Часто обе модели объединяют в одну модель Харрода-Домара. Обе модели приводят к выводу, что при данных технических условиях производства темп экономического роста определяется величиной предельной склонности к сбережению, а динамическое равновесие может существовать в условиях неполной занятости.
Ограниченность данных моделей задана уже предпосылками их анализа. Например, используемая в них производственная функция Леонтьева характеризуется отсутствием взаимозаменяемости факторов производства - труда и капитала, что в современных условиях не всегда соответствует действительности.
Модели Домара и Харрода неплохо описывали реальные процессы экономического роста 1920-1950-х гг., но для более поздних наблюдений (50-е - 70-е гг.) наиболее успешно использовалась неоклассическая модель Р. Солоу.
3. Неоклассическая модель роста Р. Солоу
Неоклассические модели роста преодолевали ряд ограничений кейнсианских моделей и позволяли более точно описать особенности макроэкономических процессов. Р.Солоу показал, что нестабильность динамического равновесия в кейнсианских моделях была следствием невзаимозаменяемости факторов производства. Вместо функции Леонтьева он использовал в своей модели производственную функцию Кобба—Дугласа, в которой труд и капитал являются субститутами. Другими предпосылками анализа в модели Солоу являются: убывающая предельная производительность капитала, постоянная отдача от масштаба, постоянная норма выбытия, отсутствие инвестиционных лагов.
Взаимозаменяемость факторов (изменение капиталовооруженности) объясняется не только технологическими условиями, но и неоклассической предпосылкой о совершенной конкуренции на рынках факторов.
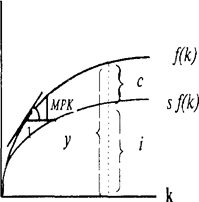
Необходимым условием равновесия экономической системы является равенство совокупного спроса и предложения. Предложение описывается производственной функцией с постоянной отдачей от масштаба: Y=F(K,L) и для любого положительного z верно: zF(K,L)= F(zK, zL). Тогда если z=1/L, тоY/L=F(K/L,1). Обозначим (Y/L) через у, а (K/L) через к и перепишем исходную функцию в форме взаимосвязи между производительностью и фондовооруженностью (капиталовооруженностью): у=ƒ(k) (см. рис. 1). Тангенс утла наклона данной производственной функции соответствует предельному продукту капитала (МРК), который убывает по мере роста фондовооруженности (k).
|
|
Рис.1
Совокупный спрос в модели Солоу определяется инвестициями и потреблением: у=i+с, где i и с - инвестиции и потребление в расчете на одного занятого. Доход делится между потреблением и сбережениями в соответствии с нормой сбережения, так что потребление можно представить как с=(1-s)y, где s -норма сбережения (накопления), тогда у=с+i=(1-s)y+i,