Рис. 1.5 Трубка Пито-Прандля.

Применение таких трубок для измерения давлений и скоростей потока в вязкой несжимаемой жидкости или газе основывается на уравнении Бернулли (1.10) для установившихся течений идеальной несжимаемой жидкости.

Уравнение Бернулли можно использовать для вычисления скорости по давлению, измеренному в так называемой «критической» точке (точке «торможения», или точке нулевой скорости) на затупленном носке трубки зонда полного напора, находящейся в установившемся потоке (см. Рис. 1.5).

В этой точке, находящейся в центре затупленной оконечности зонда (сечение 0-0) скорость потока обращается в нуль (частички воздуха ударяются в затупленный конец зонда, и тормозятся до полной остановки). В последующих точках по поверхности скорость будет расти (частички воздуха начинают огибать препятствие) и затем вновь падать, достигнув на некотором удалении от носика скорости общего потока, т.е. скорости, которая была бы в этом месте при отсутствии трубки. Эта трубка как бы не возмущает первоначальный поток

Уравнение Бернулли для сечений 1-1, 0-0 и 2-2 будет иметь вид

.

Поскольку V1 = V2, а V1 = 0, то V1 скорость должна быть равна

. (1.13)

Разность (P0 – P1) между полным и статическим давлением потока можно измерить манометром, если в критической точке (0-0) на затупленном носике трубки проделать отверстие и тонкой трубкой соединить его с одним коленом манометра, а в статическом сечении (2-2) прорезать щель, и общую с ней полость самой трубки соединить гибкой трубкой со вторым коленом манометра (см. Рис. 1.6).

Рис. 1.6 Схема подключения трубки Пито-Прандля к манометру.

Давление полного напора P0 можно измерить и отдельной трубкой (см. Рис. 1.3,а) расположив ее плотно в сечении измерения полного напора со стенкой канала.

Трубка показанная на рис 1.3,в измеряет давление P< P0 за счет срывов потока у ее хвостовой части и образования там вихрей, поэтому вычисленная величина V по разности давлений (P – P1) этой трубки не будет равна V1 (скорости потока), Однако если ввести коэффициент z , определяемый тарировкой, для этой трубки из условия

(1.14)

то, зная z, можно и этой трубкой определить V1 пo (1.13), заменяя (P0 – P1) пo (1.14). Так же можно ввести коэффициент z и для зонда другого вида. Этот коэффициент должен оставаться постоянным в определенном, достаточно большом, интервале скоростей потока - только тогда зонд пригоден для измерений в этом интервале.

1.4. Обтекание тел воздушным потоком.

При обтекании твердого тела воздушный поток подвергается деформации, что приводит к изменению скорости, давления, температуры и плотности в струйках потока. Таким образом, около поверхности обтекаемого тела создается область переменных скоростей и давлений воздуха. Наличие различных по величине давлений у поверхности твердого тела приводит к возникновению аэродинамических сил и моментов. Распределение этих сил зависит от характера обтекания тела, его положения в потоке, конфигурации тела.

Для изучения физической картины обтекания твердых тел применяются различные способы визуализации картины обтекания тела. Видимую картину обтекания тел воздушным потоком принято называть аэродинамическим спектром.

Для получения аэродинамических спектров применяют такие приборы, как дымканалы (см. Рис. 1.7, 1.8 а), используют шелковинки (Рис. 1.8 б), оптические методы исследования (для сверхзвуковых потоков) и др.

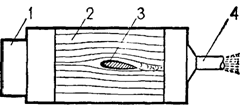
Рис. 1.7 Дымканал.

1 - источник дыма; 2 - струйки дыма; 3 - обтекаемое тело; 4 - вентилятор

В дымканале аэродинамический спектр создается струйками дыма, выпускаемыми из специального «дымаря» в поток воздуха, обтекающий тело.

Сущность способа с использованием шелковинок состоит в том, что в интересующих местах на поверхность обтекаемого тела наклеиваются специальные шелковинки, которые при обдуве тела располагаются вдоль обтекающих тело струек. По положению шелковинок судят о характере движения потока вблизи поверхности тела.

Рис. 1.8. Визуализация воздушных потоков.

а - посредством дыма, б - с нитками на транспортном средстве

Рассмотрим аэродинамические спектры некоторых тел.

Плоская пластинка (Рис. 1.9), помещенная в поток под углом 90°, создает довольно резкое изменение направления движения потока, обтекающего ее: торможение потока перед ней, поджатие струек у ее краев и образование непосредственно за краем пластинки разрежения и больших вихрей, которые заполняют всю область за пластинкой. Перед пластинкой, где в результате торможения частичек воздуха и падения их скорости до нуля (кинетической энергии воздушного потока полностью переходит в потенциальную), давление (по уравнению Бернулли) будет больше чем в невозмущенном потоке, а за пластинкой вследствие разрежения давление уменьшится.

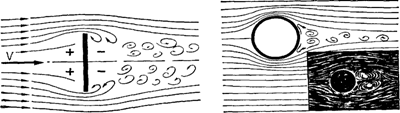
Рис. 1.9 Аэродинамический спектр плоской пластинки и шара.

Может быть, шар - идеально обтекаемая поверхность? Нет! Действительно, сначала воздух легко обтекает закругленную поверхность шара. Но когда воздушный поток минует точку, где шар имеет максимальный радиус, ему придется следовать за стремительно сходящейся поверхностью. Для воздуха эта задача более трудная, и вскоре воздушный поток будет уже не в состоянии следовать за поверхностью и оторвется от нее, вызывая турбулентные завихрения. Турбулентные завихрения беспорядочно движутся с обратной стороны шара. Давление турбулентного воздуха ниже, чем окружающего спокойного, и поэтому возникает сила всасывания, действующая в обратном относительно движения шара направлении и тормозящая его.

Симметричное каплеобразное тело (Рис. 1.10), имеет более плавный характер обтекания, как в передней, так и в хвостовой частях.

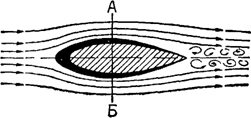
Рис. 1.10 Аэродинамический спектр каплеобразного тела.

Воздух с легкостью огибает его переднюю закругленную часть, но там, где у шара воздух уже не может следовать за изгибом поверхности и отрывается от нее, у каплеобразного объекта поверхность поката, и воздух легко ее огибает, вызывая очень маленькое торможение.

В сечении А - Б (наибольшая величина поперечного сечения) аэродинамический спектр показывает наибольшую деформацию струек, наибольшее их поджатие. В хвостовой части образуются небольшие завихрения потока, которые уносятся потоком, постепенно затухая (Рис. 1.10).