рис. 1

Газовый термометр представляет собой стеклянный, кварцевый или металлический баллон неизменного объема, заполненный реальным газом и соединённый с помощью капилляра с манометром. Уровень ртути в левом колене манометра доводится до отметки О, чтобы обеспечить постоянство объёма газа. В качестве рабочего раза раньше употреблялся водород. Сейчас же в основном употребляется гелий (для измерения низких и средних температур) и азот (для измерения высоких температур, где гелий не пригоден, т.к. он легко диффундирует сквозь стенки баллона). Давление газа измеряется по манометру, и затем, по этому давлению вычисляется температура с учётом поправок на изменение объёма баллона, неидеальность газа и пр.

Несмотря на кажущуюся простоту измерение температуры с помощью газового термометра – нелёгкая экспериментальная работа, требующая от экспериментатора особой тщательности. Поэтому в повседневной жизни пользуются другими типами термометров. Идеально – газовым термометром пользуются в исключительных случаях, когда нужна высокая точность измерения температуры.

Интервал, измеряемых газовым термометром, температур ограничен. Это связано с тем, что все реальные газы при очень низких температурах конденсируются и далее уже не подчиняются закону Бойля – Мариотта. Точно также при очень высоких температурах молекулы газа начинают диссоциировать (распадаться) на электроны и положительно заряженные ионы и также перестают подчиняться закону Бойля – Мариотта.

Но всё же там, где пригодна газовая шкала, она практически не отличается от шкалы Кельвина. Поэтому в интервале температур от 4 К до 1338 К абсолютная термодинамическая шкала осуществляется именно с помощью газового термометра.

Газовая шкала, хотя и слабо, но всё же зависит от природы рабочего газа. Рациональная температурная шкала не должна зависеть от свойств термометрического вещества. Этим требованиям удовлетворяет абсолютная термодинамическая шкала Кельвина. Хотя она и не относится к экспериментальным шкалам, но она так важна в физике, что я посчитал необходимым упомянуть и её.

Термодинамическая абсолютная шкала Кельвина.

В 1848 г. Вильям Томсон (лорд Кельвин) указал, что теоремой Карно можно воспользоваться для построения рациональной темпе­ратурной шкалы, совершенно не зависящей от индивидуальных осо­бенностей термометрического вещества и устройства термометра.

Из теоремы Карно следует, что КПД цикла Карно может зави­сеть только от температур нагревателя и холодильника. Обозначим буквами t1 и t2 эмпирические температуры нагревателя и холодиль­ника, измеренные каким-либо термометром (например, газовым, ртутным, термометром сопротивления и т. п.). Тогда

где f(t1, t2) — универсальная функция выбранных эмпирических температур t1 и t2. Ее вид совершенно не зависит от устройства ма­шины Карно и от рода используемого рабочего вещества. Этим об­стоятельством и воспользовался Вильям Томсон, предложивший применить цикл Карно для построения температурной шкалы.

Чтобы построить термодинамическую шкалу температур, введем более простую универсальную функцию температур t1 и t2:

Эта функция легко выражается через прежнюю функцию f(t1,, t2). Определим общий вид функции φ(t1,, t2). С этой целью возьмем три тепловых резервуара, температуры которых поддерживаются посто­янными. Эмпирические температуры этих резервуаров обозначим че­рез t1, t2, t3 соответственно. Используя их в качестве нагревателей и холодильников, проведем три цикла Карно, изображенные на рис. 26.

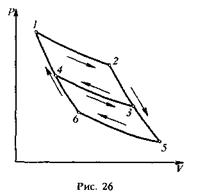
Предполагается, что t1, t2, t3 — тем­пературы на изотермах 12, 43, 65. Для циклов Карно 1234 и 4356 можно написать

Исключив отсюда теплоту Q2, полу­чим

Но эти два цикла, объединенные вместе по схеме рис. 26, эквивалент­ны одному циклу Карно 1256. Это

происходит потому, что по изотерме 43 мы проходим дважды в проти­воположных направлениях, и она может быть исключена из рассмот­рения. Следовательно,

Сравнивая это соотношение с предыдущим, получим

Такое соотношение справедливо при любом значении аргумента t3. Левая часть его не зависит от значения температуры t3. Поэтому и отношение в правой части не может меняться с изменением t3. Можно фиксировать t3 , не меняя значения самого отношения. Но тогда числитель в правой части формулы (31.5) будет функцией од­ного только аргумента t1. Обозначим эту функцию через Θ(t1). Зна­менатель будет такой же функцией, но от аргумента t2.

Итак,

Таким образом, φ(t1,, t2) есть отношение значений одной и той же функции Θ (t). Так как величина Θ(t) зависит только от температуры, то она сама может быть принята за меру температуры тела. Величину Θ(t) и называют абсолютной термо­динамической температурой. Отношение двух термодинамических температур Θ1 ≡ Θ1(t) и Θ2 ≡ Θ2(t) определяется соотношением

3. Отношение Θ1/ в принципе может быть найдено экспери­ментально. Для этого надо измерить теплоты Q1 и Q2. Однако зна­чением этого отношения сами температуры Θ1, Θ2 и еще не опреде­ляются однозначно. Это видно также из того, что функция Θ(t) = φ( t1,, t2) зависит от параметра t3, которому можно придать произвольное значение. Отношение не зависит от параметра t3. Однако сами термодинамические температуры будут иметь раз­ные значения при различном выборе этого параметра. Вместо функ­ции Θ (t) можно было бы в качестве термодинамической температу­ры принять, например, величину Θ' (t) = ψ(t3)Θ(t), где ψ(t3) — произвольная функция. От этого значение отношения не из­менилось бы. Но, придавая параметру t3 различные значения, мы получили бы бесконечное множество температурных шкал, отли­чающихся друг от друга масштабами единицы температуры. Чтобы однозначно определить термодинамическую температуру Θ, можно поступить двояко.

Во-первых, можно взять какие-либо две постоянные темпера­турные точки, например нормальную точку плавления льда и нор­мальную точку кипения воды. Обозначим термодинамические тем­пературы этих точек Θп и, а соответствующие им количества теплоты в цикле Карно — Qп и Qк. Фиксируем далее значение разности Θп - Θк , например примем, что она равна 100 градусам. Тог­да температурный интервал между нормальными точками плавле­ния льда и кипения воды разделится на 100 равных частей, каждая из которых ранее называлась градусом Кельвина, а теперь — просто Кельвином. Из двух уравнений