Чтобы ясен был многоликий характер понятия “канал связи”, достаточно привести несколько примеров.

При телефонной передаче источник сообщения - говорящий. Кодирующее устройство, изменяющее звуки слов в электрические импульсы, - это микрофон. Канал, по которому передается информация - телефонный провод. Та часть трубки, которую мы подносим к уху, выполняет роль декодирующего устройства. Здесь электрические сигналы снова преобразуются в звуки. И наконец, информация поступает в “принимающее устройство”-ухо человека на другом конце провода. А вот канал связи совершенно другой природы - живой нерв. Здесь все сообщения передаются нервным импульсом. Но в технических каналах связи направление передачи информации может меняться, а по нервной системе передача идет в одном направлении.

Еще один пример - вычислительная машина. И здесь те же характерные черты. Отдельные системы вычислительной машины передают одна другой информацию с помощью сигналов. Ведь вычислительная машина -автоматическое устройство для обработки информации, как станок - устройство для обработки металла. Машина не создает из “ничего” информацию, она преобразует только то, что в нее введено.

канал связи

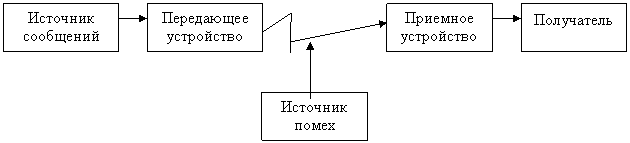Рис.1.Общая схема передачи информации.

4. Измерение информации.

Какое количество информации содержится, к примеру, в тексте романа "Война и мир", в фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро.

А возможно ли объективно измерить количество информации? Важнейшим результатом теории информации является вывод:

В определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных.

В настоящее время получили распространение подходы к определению понятия "количество информации", основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте.

Так, американский инженер Р. Хартли (1928 г.) процесс получения информации рассматривает как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определяет как двоичный логарифм N.

Формула Хартли: I = log2N.

Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 ” 6,644. То есть сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единиц информации.

Приведем другие примеры равновероятных сообщений:

при бросании монеты: "выпала решка", "выпал орел";

на странице книги: "количество букв чётное", "количество букв нечётное".

Определим теперь, являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.

Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.

Формула Шеннона: I = – ( p1 log2 p1 + p2 log2 p2 + . . . + pN log2 pN ),

где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.

Легко заметить, что если вероятности p1, ., pN равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.

Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями.

В качестве единицы информации условились принять один бит (англ. bit — binary, digit — двоичная цифра).

Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений.

А в вычислительной технике битом называют наименьшую "порцию" памяти, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд.

Бит — слишком мелкая единица измерения. На практике чаще применяется более крупная единица — байт, равная восьми битам. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=28).

Широко используются также ещё более крупные производные единицы информации:

1 Килобайт (Кбайт) = 1024 байт = 210 байт,

1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт,

1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт.

В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:

1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт,

1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.

За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации.

5. Использование информации.

Информацию можно: создавать, передавать, воспринимать, иcпользовать, запоминать, принимать, копировать, формализовать, распространять, преобразовывать, комбинировать, обрабатывать, делить на части, упрощать, собирать, хранить, искать, измерять, разрушать, и др.

Все эти процессы, связанные с определенными операциями над информацией, называются информационными процессами.

6. Свойства информации.

Информация обладает следующими свойствами, характеризующими ее качественные признаки: достоверность, полнота, ценность, своевременность, понятность, доступность, краткость и др.

Информация достоверна, если она отражает истинное положение дел. Недостоверная информация может привести к неправильному пониманию или принятию неправильных решений.

Достоверная информация со временем может стать недостоверной, так как она обладает свойством устаревать, то есть перестаёт отражать истинное положение дел.

Информация полна, если её достаточно для понимания и принятия решений. Как неполная, так и избыточная информация сдерживает принятие решений или может повлечь ошибки.

Точность информации определяется степенью ее близости к реальному состоянию объекта, процесса, явления и т.п.

Ценность информации зависит от того, насколько она важна для решения задачи, а также от того, насколько в дальнейшем она найдёт применение в каких-либо видах деятельности человека.