Примером такого отношения может служить отношение "больше- меньше", определяющее структуру бинарного дихотомического дере­ва. В таком дереве все вершины любого правого поддерева имеют значение инфор­маци­он­ного поля большее, чем значение такого же по­ля у корня, а веp­ши­ны соответствующего левого поддерева – мень­шее. Например, конструирование дихото­ми­ческого дерева по пос­ледовательности целых чисел 30, 70, 80, 21, 25, 17, 4, начиная с 30, должно приводить к созданию следующей структуры:

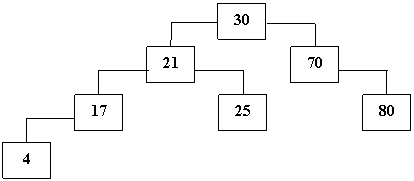
Рис. 3

Нетрудно заметить, что процесс конструирования такого дерева про­исходит сверху вниз, начиная с корня, путем последовательного сравнения числовых значений, размещаемых в вершинах, с целью определения места размещения соответствующей вершины в структуре дерева. Любая модификация дихотомического дерева (удаление вершины, вставка новой веpшины) не должна нарушать дихотомической структуры в целом.

В об­щем случае трансформация произвольной информационной строки (пос­ледо­ва­тель­ности объектов) в структуру дерева и об­рат­но основана на использовании глубоких структурных межобъектных отно­шений в исходной строке. Такая трансформация позволяет наг­ляд­­но представить подобные отношения в форме дерева. В программировании дерево во многом рассматривается как формальная структура, наполняемая различным семантическим содержанием. Такой под­ход позволяет формально реализовать многие преобразования дан­ных на основе унифицированных процедур обхода деревьев.

Нап­ри­мер, в теории трансляции широко используется понятие Поль­ской инверсной записи (ПОЛИЗ) – особой системы представления математических выражений символьными последовательностями. Так, например, выражение " a + b * c " будет представлено в ПОЛИЗЕ строкой " a b c * + ". Если представить исходное выражение в естественной иерархической форме бинарного дерева :

Рис. 4

то его восходящий обход (пунктир на рис. 4) приведет к стро­ке " a b c * + ", определяющей "польский" эквивалент исходной стро­ки. Формула восходящего обхода "Левый–Правый–Корень" (ЛПК) определяет правило обхода бинарного дерева: восходящий об­ход связан с обходом его левого поддерева, затем правого под­де­ре­ва, затем корня. Поскольку каждая вершина дерева может интер­пре­­тироваться как корень "вырастающего из нее" поддерева, это пра­­вило применяется рекурсивно к каждой вершине обходимого де­ре­ва. Правило ЛКП (Левый–Корень–Правый) определяет так на­зы­ва­е­­мый смешанный обход, правило КЛП – нисходящий обход и т.д. Нет­ру­дно заметить, что смешанный обход дерева дихотомии по пра­вилу ЛКП приведет к формированию строки чисел (хранящихся в вершинах этого дерева), упорядоченной по возрастанию, а такой же обход по правилу ПКЛ – к формированию строки, упорядоченной по убыванию соответствующих чисел. Таким образом, между структурой дерева, от­ношением порядка на множестве информационных компонент его вер­шин и видом обхода существует глубокая связь, определяемая ре­­курсивной природой структуры дерева. Рекурсивные процедуры об­хо­да бинарных деревьев пишутся прямо по формуле обхода с учетом спе­цификации представления вершин дерева. Например, ниже при­ве­де­на процедура смешанного обхода бинарного дерева дихотомии, ре­а­лизующего формулу ЛКП.

TYPE Вершина = POINTER TO Элемент ;

Элемент = RECORD

Info : CARDINAL ;

LLink,RLink : Вершина

END ;

PROCEDURE Смеш_Обход (K : Вершина);

BEGIN

IF K # NIL THEN

Смеш_Обход (K^.LLink); (* Обход левого поддерева *)

WriteCard (K^.Info); (* Обработка корня *)

Смеш_Обход (K^.RLink); (* Обход правого поддерева *)

END

END Смеш_Обход.

В традиционном программировании рекурсия часто рас­сма­три­ва­ет­ся как некоторый заменитель итерации. Причем в качестве примеров рас­сматривается вычисление рекуррентных последовательностей, ко­то­рые могут быть легко сформированы и обычными итераторами (цик­ла­ми WHILE, REPEAT и т.п.). Природа рекурсии значительно глубже, чем механизм итерации, поэтому ее использование практически не име­ет альтернатив в виде итераторов только тогда, когда решение за­дач проводится на рекурсивных структурах. Попробуйте написать про­цедуру Смеш-Обход без использования рекурсии, только на ос­но­ве циклов и, если Вам это удастся, сравните ее с приведенным вы­ше вариантом рекурсивной процедуры по наглядности, лаконичности, вы­разительности.

1.5. Примеры решения задач с помощью рекурсии

1.5.1. “Ханойская башня”

При написании рекурсивных программ, следует помнить, что при рекурсивном вызове процедурой самой себя или другой процедуры следует соблюдать определённые “правила предосторожности”. Рекомендуется компилировать программу с директивой {$S+}. Эта директива включает проверку переполнения стека (области памяти, в которой хранится состояние вызывающей подпрограммы). Если в процессе выполнения программы происходит переполнение стека, вызов процедуры или функции, откомпилированной с опцией {$S+}, приводит к завершению работы программы, а на дисплей выдаётся сообщение об ошибке. Полезно также использовать директиву {$R+}, включающую проверку диапазона переменных. В начале каждой процедуры (функции), вызываемой рекурсивно, можно разместить строку if keypressed then Halt. В этом случае при зависании программы вместо перезагрузки будет достаточно нажать любую клавишу.

Количество рекурсивных вызовов называется глубиной рекурсии. Глубина рекурсии должна быть конечной. Позаботиться об этом должен программист, выбирающий или разрабатывающий рекурсивный алгоритм.

Рассмотрим пример. Правила головоломки “Ханойская башня” таковы. Имеется доска с тремя колышками. На первом из них нанизано несколько дисков убывающего диаметра (самый большой находится внизу – рис. 5).