Пусть А и В – нечеткие множества на Х, и - их функции принадлежности соответственно.

Говорят, что А включает в себя В (то есть ), если для любого выполняется неравенство (Рис.9.2.).

Если , то .

Множества А,В эквивалентны (А~В), если

Пример. Рассмотрим нечеткие множества

Тогда и функции принадлежности этих множеств должны удовлетворять условию

Операции над нечеткими множествами.

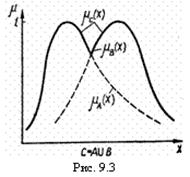
Определение 5. Объединением нечетких множеств А и В в Х называется нечеткое множество с функцией принадлежности вида (Рис.9.3.)

Определение 6. Сильным объединением нечетких множеств А и В в Х называется нечеткое множество с функцией принадлежности

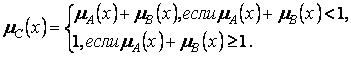
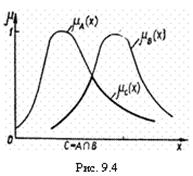
Определение 7. Пересечением нечетких множеств А и В в Х называется нечеткое множество с функцией принадлежности вида (Рис.9.4.).

Если - конечное или бесконечное семейство нечетких множеств с функциями принадлежности , где - параметр семейства, то пересечение является нечетким множеством с функцией принадлежности вида .

Определение 8. Сильное пересечение нечетких множеств А и В в Х определяется как нечеткое множество с функцией принадлежности вида

Определение 9. Разностью нечетких множеств А и В в Х называется нечеткое множество А\В с функцией принадлежности вида

Определение 10. Декартовым произведением нечетких множеств А2 в называется нечеткое множество в декартовом произведении с функцией принадлежности вида

Определение 11. Выпуклой комбинацией нечетких множеств на Х называется нечеткое множество А с функцией принадлежности вида

, где

Определение 12. Операции концентрирования и растяжения нечеткого множества А определяется следующим образом:

Или в общем случае

где целое