Следовательно, групповой показатель по экономическим параметрам для первой модели равен:

,

так как в течение Т = 4 года, Е = 14%, С0, С1 всегда были постоянны и равны соответственно С0 = 1,38, а С1 = 0,81, то С0 и С1 можно вынести за знак суммы и тогда групповой показатель по экономическим параметрам будет рассчитываться по формуле:

для второй модели:

для третьей модели:

2.3.3. Расчет интегрального показателя.

Интегральный показатель конкурентоспособности рассчитывается по формуле (2.11):

,

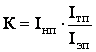но так как групповой показатель по нормативным параметрам не указан, то в расчете интегрального показателя он не будет учитываться и формула примет вид: ,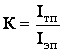

Тогда для первой модели:

для второй модели:

для третьей модели:

2.4. Анализ результатов расчета

В результате полученных групповых показателей по техническим параметрам третья модель компьютеров наиболее конкурентоспособная, то есть в целом третья модель компьютеров полнее удовлетворяет запросы потребителя, чем все остальные модели компьютеров. Так как групповой показатель характеризует степень соответствия исследуемого изделия соответствующим потребностям по всем техническим параметрам (для данного случая: быстродействие, объем памяти, качество обслуживания).

А из полученных расчетов по экономическим параметрам видно, что первая модель компьютеров более конкурентоспособная по экономическим параметрам из всех остальных моделей компьютеров, так как имеет самый маленький групповой показатель, который у первой модели равен 0,629. А это значит, что покупатель будет с большей охотой покупать первую модель компьютеров, чем все остальные. Но так как срок морального старения у компьютеров очень маленький, то выгоднее покупать третью модель. Хоть она и дороже, но по техническим параметрам она вполне конкурентоспособная.

Из расчетов интегрального показателя конкурентоспособности видно, что первая и вторая модели компьютеров уступают образцу по конкурентоспособности в целом, так как у них интегральный показатель меньше единицы. А третья модель превосходит образец по конкурентоспособности в целом, потому что у нее интегральный показатель больше единицы и равен 1,147. Это говорит о том, что для российских покупателей выгоднее покупать третью модель, так как она по техническим параметрам не уступает образцу, а ее стоимость гораздо меньше.

3. ОРГАНИЗАЦИОННО - ЭКОНОМИЧЕСКИЙ РАЗДЕЛ

3.1. Расчет интегрального показателя конкурентоспособности компьютера

«ВИСТ» по годам

Так как в мире постоянно появляется что-то новое и ничто не стоит на месте, то за определенное время произошли некоторые изменения и в компьютерных технологиях. Поэтому необходимо проанализировать изменения уровня конкурентоспособности компьютеров. Это можно выяснить, рассчитав индекс конкурентоспособности по годам:

(3.1)

Таблица 3.1.

Основные характеристики сравниваемых компьютеров первой модели

Рассчитаем для первой модели компьютеров 1996 и 1997 годов выпуска групповой показатель по техническим параметрам, который рассчитывается по формуле (2.5):

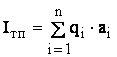
Для данного случая формула (2.5) принимает вид:

Iтп = q1·a1 + q2·a2 + q3·a3,

где q1, q2, q3, рассчитываются по формуле (2.1):

Значит для первой модели 1996 года выпуска:

Iтп = 0,30·0,75 + 0,50·0,50 + 0,84·0,20 = 0,643;

а для первой модели 1997 года выпуска:

Iтп = 0,30·0,75 + 0,50·0,50 + 0,76·0,20 = 0,627

Из расчетов видно, что групповой показатель по техническим параметрам уменьшился за год.

Теперь рассчитаем для этих телевизоров групповой показатель по экономическим параметрам, который рассчитывается по формуле (2.10):

,

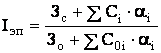так как Сi и Со постоянны, то формула принимает вид:

,