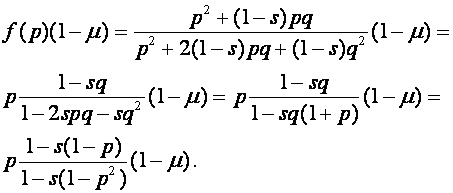
Далее,

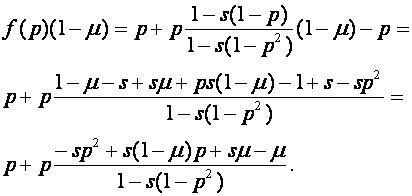
Тем самым, отображение (24) приобретает вид:

.

Одна из неподвижных точек отображения, очевидно, . Две другие определяются из уравнения:

.

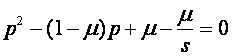Получаем:

, .

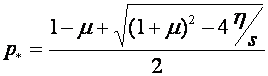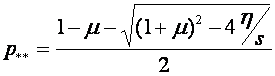Оба корня существуют поскольку .Здесь . Поскольку для , то знак разности определяется знаком квадратного трехчлена . Если , то . Если же , то . Наконец, для . (См. Рисунок.)Тем самым, при начальной точке траектории при . Состояние полиморфизма , устойчиво (полиморфизм балансирован). Соответственно, состояние равновесия неустойчиво. Если начальная точка, то соответствующая траектория стремится к нулю. Однако, нужно заметить, что здесь мы выходим за рамки применимости модели. При больших концентрациях аллеля нужно учитывать мутации от аллелей к аллелям .