Определение.

Пусть G- абелева группа и - система ее подгрупп. G называется прямой суммой системы подгрупп, если каждый элемент однозначно представляется в виде суммы , где . Это записывается следующим образом: .

Таким образом, диагональный вид матрицы означает, что , где количество слагаемых Z равно n-r . Очевидно, что слагаемые, отвечающие тривиальным группам (d=1) могут быть исключены из этой суммы.

Примеры.

1. Очевидно, что .

2. Отметим, что если все подгруппы имеют конечные порядки , то порядок равен .

3. Подгруппа состоит из элементов: , а - из элементов . Поскольку += и +=, мы видим, что .

4. В развитие предыдущего примера установим, что, если числа p и q взаимно просты, то. Используем основную теорему теории делимости: существуют целые x и y, такие что 1=xp+yq . Отсюда для любого n получаем, что n=nyq+nxp и значит . Остается заметить, что эти группы имеют одинаковые порядки.

5. Как было показано на предыдущей лекции, группа описывается матрицей 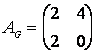. Приводя эту матрицу к диагональному виду, получаем эквивалентную матрицу . Следовательно, . В качестве образующих этих циклических подгрупп можно взять, например, элементы и .

Подводя итог всему вышесказанному, можно утверждать, что всякая г.к.о. G является прямой суммой своих циклических подгрупп , (1)

где порядки конечных подгрупп удовлетворяют условию: числа - целые. Разложение (1) называется первым каноническим разложением группы G.