Если ее переписать в виде

**************************

Доказательство:

Рассмотрим вспомогательную ф-ию .

1. Она непрерывна на как сумма непрерывных ф-ий.

2. F(x) – дифф. на как сумма дифф. на интервале ф-ий.

3. F(а) = 0; F(b) = 0

Sl: Пусть ф-ия дифф. на , тогда для любой внутренней точки интервала справедлива формула Лагранжа:

х0 между

Действительно ***************

Из дифф. ф-ии на следует ее непрерывность на

Теорема Коши: Пусть и :

1. Непрерывны на .

2. Дифф. на

Тогда на существует т. х0 , для которой справедлива формула Коши:

Доказывается как теорема Лагранжа.

Приложение производной к исследованию ф-ий.

1. Исследование на монотонность.

Пусть дифф. на , тогда справедливо:

· Ф-ия возрастает на на .

· Ф-ия не убывает на на .

· Ф-ия постоянна на на .

· Ф-ия не возрастает на на .

· Ф-ия убывает на на .

2. Исследование на экстремум.

Df: т. х0 называется точкой локального минимума, если ф-ия непрерывна в этой точке и существует такая окрестность х0 , что для любого х

**************************

Исследование ф-ии на выпуклость графика.

**************************

Df: График ф-ии на направлен выпуклостью вниз (вогнутый), если он расположен выше касательной, проведенной в любой точке , а график ф-ии - выпуклый, если он расположен ниже касательной, проведенной в любой точке .

Df2: Точка х0 , в которой непрерывна, называется точкой перегиба, если она отделяет интервал выпуклости от интервала вогнутости.

Достаточные условия выпуклости ф-ии на интервале.

Пусть ф-ия дважды дифф. на и сохраняет на нем свой знак, то:

1. , то график на- вогнутый.

2. , то график на- выпуклый.

Асимптоты графика ф-ии.

В некоторых случаях, когда график ф-ии имеет бесконечные ветви, оказывается, что при удалении точки вдоль ветви к бесконечности, она неограниченно стремится к некоторой прямой. Такие прямые называют асимптотами.

.Вертикальные асимптоты – прямая называется вертикальной асимптотой графика ф-ии в точке b , если хотя бы один из разносторонних пределов равен бесконечности.

Если ф-ия задана дробно-рациональным выражением, то вертикальная асимптота появляется в тех точках, когда знаменатель равен нулю, а числитель не равен нулю.

********************

Наклонная асимптота – прямая наклонная асимптота ф-ии , если эта ф-ия представлена в виде

Необходимый и достаточный признак существования наклонной асимптоты:

Для существования наклонной асимптоты к графику ф-ии необходимо и достаточно существование конечных пределов:

Доказательство: Пусть:

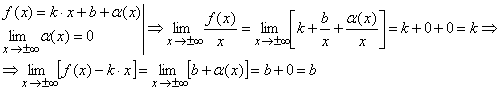
Пусть:

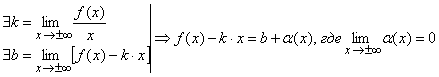
Следовательно существует асимптота.

Общая схема исследования ф-ий

1. По ф-ии

1.1. D(f)

1.2. E(f)

1.3. Непрерывность в области определения

1.4. Четность, нечетность.

1.5. Переодичность

1.6. Асимптоты

2. По первой производной

2.1. Экстремумы

2.2. Интервалы монотонности

3. По второй производной

3.1. Интервалы выпуклостей

3.2. Точки перегиба

4. Построение графика ф-ии.

Приложение производной к вычислению пределов.

(Правило Лопиталя).